

Som nybörjare lär man sig inte programmera genom att enbart läsa eller lyssna. Med detta undervisningsmaterial är det därför tänkt att du ska köra de exempel som finns i texten parallellt med att du läser. Exemplen är korta och du kan i många fall kopiera ett stycke kod, klistra in i editorn och sedan göra någon mindre ändring.
För en fullständig referens av Python kan du se på sidan Python 3.6.7 documentation. På den sidan kan du i det övre vänstra hörnet välja Python-version.
Börja med att göra ett konto på https://repl.it. Klicka sedan på Start coding now. Välj Python i listan som dyker upp, då skapas ditt Python-program.
Skriv in koden:
print("Välkommen!")i editeringsfönstret (det mittersta fönstret) och klicka sedan på run. Koden körs i den svarta konsolen till höger.
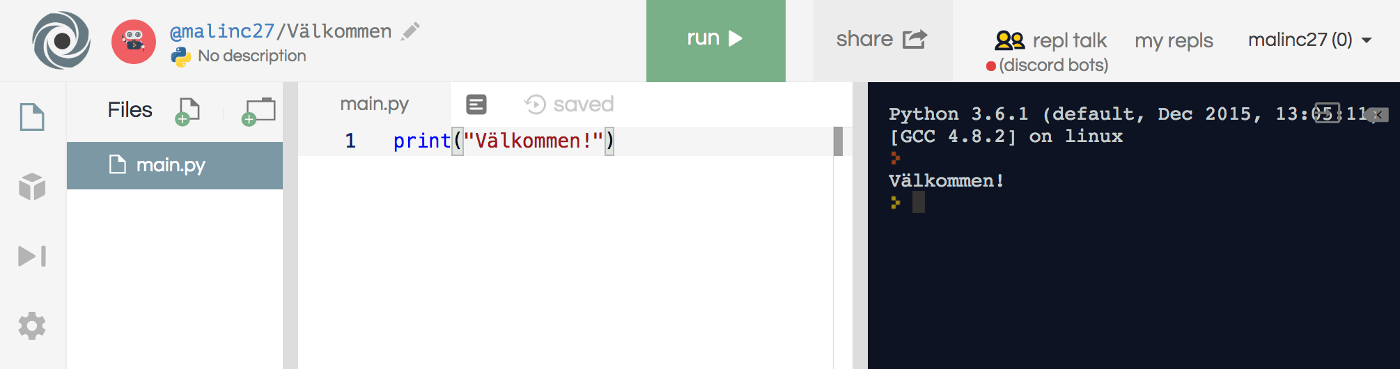
Om du vill göra ett nytt program, klickar du på ikonen i det övre vänstra hörnet. Därefter klickar du på den stora röda ikonen med ett plus-tecken i det nedre högra hörnet.

Den svarta konsolen till höger används inte bara till att visa utskrifter från program. I konsolen körs ett program kallat Python Shell vilket gör det möjligt att använda konsolen på ett interaktivt sätt. Du kan skriva kod i konsolen. Python Shell ser till att Python interpretatorn översätter koden till exekverbar kod och sedan kör koden. Därefter skrivs resultatet ut.
En programmeringsmiljö som Python Shell kan kallas för REPL vilket står för Read Eval Print Loop.
Man kan använda Python Shell som en miniräknare. De aritmetiska operatorerna i Python är:
| operator | operation | exempelkod | resultat |
|---|---|---|---|
+ - * / |
de fyra räknesätten | 4.3+2.7 |
7.0 |
** |
upphöjt till | 2**3 |
8 |
% |
resten vid heltalsdivision | 20%6 |
2 |
// |
kvoten vid heltalsdivision | 20//6 |
3 |
Prioritetsordningen när aritmetisk uttryck beräknas är
Beräkningen 15-6*2 ger resultatet 3.
Beräkningen (15-6)*2 ger resultatet 18.
Utför beräkningen 2*3**2 i Python Shell. Vilken av operatorerna * och ** används först?
(Det operatorn // egentligen gör är att avrunda genom att ta bort decimalerna.)
Variabler används för att lagra värden som kan användas i programmet. En variabel har ett namn och ett värde. Att ge en variabel ett värde kallas för att tilldela den ett värde.
Man inför en variabel genom att ge den ett namn och tilldelar den ett värde med hjälp av likhetstecken. Likhetstecknet används alltså inte som likhet utan för en tilldelning.
Skriv in a = 7 och klicka på enter. Skriv sedan a för att se variabeln a's värde.
Skriv a = a + 1 upprepade gånger. Visa sedan vilket värde variabeln a har. Du kan klicka på tangenten pil upp för att få fram tidigare skrivna kommandon.
Genom att använda sig av pil-upp- och pil-ner-tangenterna kan man stega sig igenom gamla kommandon i Python Shell.
Skrivsättet a = a + 1 är en tilldelning som fungerar på så vis att först beräknas det som står till höger om likhetstecknet. Sedan tilldelas a detta nya värde.
Python håller reda på vilken datatyp en variabel är. Du kan använda funktionen type() för att ta reda på vilken datatyp en variabel är.
Skriv in de tre variablerna a = 15, b = 2.7 och c = "Hej!" i Python Shell.
Skriv sedan type(a), type(b) och type(c).
Det är inget problem att byta datatyp. Testa att skriva a = "Huh?" och sedan type(a).
Datatypen int står för integer dvs heltal.
Datatypen float står för floating point vilket heter flyttal på svenska. Flyttal är den datatyp som används för decimaltal.
Datatypen str står för string vilket kallas för textsträng på svenska.
Utöver dessa tre datatyper finns det också en datatyp kallad bool som står för Boolean eller boolesk på svenska. Den booleska datatypen används för logiska värden, dvs värden som antingen är sanna eller falska. Denna datatyp är uppkallad efter George Boole som uppfann den så kallade booleska algebran.
Ett booleskt värde i Python har antingen värdet True eller False. Ett booleskt värde är ett logiskt värde.
De logiska operatorerna i Python är:
| operator | logisk operation |
|---|---|
and |
och |
or |
eller |
not |
inte |
De logiska operatorerna verkar på logiska värden och resultatet är ett logiskt värde.
Numeriska jämförelser kan användas till att skapa logiska värden. Jämförelseoperatorerna är:
| operator | jämförelse |
|---|---|
== |
lika med |
!= |
skilt från |
< |
mindre än |
<= |
mindre än eller lika med |
> |
större än |
>= |
större än eller lika med |
En jämförelseoperator verkar på tal och resultatet är ett logiskt värde. Lägg märke till att dubbla likhetstecken används för likhet eftersom enkelt likhetstecken används för tilldelningar.
Testa att skriva in variabler med boolska värden och booleska uttryck i Python Shell, exempelvis
a = 5 < 7,
b = False,
a and b,
not b,
a or 3*4 >= 12,
c = 0 < 5 < 10.
Textsträngar består av tecken inneslutna av antingen citationstecken (") eller apostrof ('). Vill du att en textsträng skall innehålla en apostrof kan du välja citationstecken som avdelare, och vice versa.
Gör en variabel a med värdet: "Eureka" he shouted.
Låt textsträngen inneslutas av apostrofer.
Gör en variabel b med värdet:
It's called Archimedes' principle.
Låt textsträngen inneslutas av citationstecken.
Testa att skriva 3*a.
Testa att skriva 3+a.
Testa att skriva a+b.
Testa att skriva a*b.
Python Shell kan vara behändigt för att snabbt se olika sorters utdata. För längre stycken kod är det dock enklare att använda editorn. Vi kommer hädanefter att skriva koden i editorn och köra koden genom att klicka på run
När man skriver kod i editorn visar man utdata med funktionen print(). Funktionen print() kan ta emot flera argument och argumenten skrivs ut separerade av ett blanktecken.
Koden:
a = 7
b = 13
print("a = ", a)
print("b = ", b)
print("summan är", a+b)Ger utskriften:
a = 7 b = 13 summan är 20
Funktionen print() avslutar en utskrift genom att göra en radbrytning. Man kan välja att avsluta en utskrift på annat sätt med hjälp av den speciella parametern end, denna parameter kan sättas till något annat än radbrytning, exempelvis ett blanktecken. Det finns också en speciell parameter sep som används för att separera utskriften av de olika argumenten. Man kan ange att sep ska vara något annat än ett blanktecken.
Koden:
a = 7
b = 13
print("a = ", a, end = " ")
print("b = ", b)
print("summan är", a+b, sep ="")Ger utskriften:
a = 7 b = 13 summan är20
Ser du skillnaden mellan utskrifterna?
För att ta emot indata använder du funktionen input(), som argument skriver du den text som ska visas. Funktionen input() returnerar det användaren svarat i en textsträng. Detta svar lagras lämpligen i en variabel, exempelvis som koden:
namn = input("Vad heter du?")
print("Hej", namn)Om du vill att användaren ska mata in numeriska värden som ska användas i numeriska uttryck, måste du omvandla textsträngen till en numerisk datatyp. Det finns ett antal inbyggda funktioner för omvandling mellan datatyper.
int() omvandlar till ett heltal.float() omvandlar till ett flyttal.str() omvandlar till en textsträng.Det finns en lista med alla inbyggda funktioner på sidan Python: Built-in Functions.
Testa koden:
# Addera två heltal.
atxt = input("a =") #läs in som textsträng
btxt = input("b =")
a = int(atxt) #omvandla till heltal
b = int(btxt)
summa = a+b
print("a+b =",summa)Ändra sedan koden till:
# Addera två heltal.
a = int(input("a =")) #läs in som textsträng och omvandla till heltal
b = int(input("b ="))
summa = a+b
print("a+b =",summa)Det som står efter tecknet # är så kallade kommentarer. Kommentarer exekveras inte utan är till för den som läser koden.
Ändra i koden så att två flyttal adderas. Testkör programmet och mata in två flyttal. Tänk på att använda decimalpunkt istället för decimalkomma.
Funktionen print() omvandlar automatiskt alla argument till textsträngar. Funktionen input() däremot tar bara emot ett argument som är en textsträng.
Om du vill sätta samman en textsträng som du själv skriver i koden med en variabels värde, omvandlar du först variabelvärdet till en textsträng, sedan sätter du samman textsträngarna med hjälp av tecknet +. Att sätta samman textsträngar på det här viset kallas för att konkatenera.
(Senare ska vi se hur kan man sätta samman variabelvärden med textsträngar genom att istället formatera textsträngar på olika sätt.)
a = 3
b = 7
svar = int(input("Vad är " + str(a) + "*" + str(b) + "?"))För att kunna ställa en fråga och sedan låta programmet svara "rätt" eller "fel" behövs en programmeringsstruktur som kallas villkorssats.
En villkorssats används om programmet ska utföra olika saker beroende på om något villkor är sant eller falskt. En villkorssats kan också kallas för en selektion eller ett alternativ. Det är också mycket vanligt att man kallar villkorssatser för if-satser eller if-else-satser.
En enkel if-sats i Python skriv som
if <villkor>:
# indenterad kod som ska utföras om villkoret santDen kod som ska utföras om villkoret är sant, måste indenteras, dvs den måste dras in. Editorn som används av repl.it indenterar automatiskt på raden efter ett kolon. All kod som är indenterad efter if-satsens kolon utförs om villkoret är sant.
Platshållare i kodexemplen
Den rosa text som står mellan < och > i alla kodexempel är så kallade platshållare och ska ersättas av variabler eller uttryck. Platshållaren
<villkor>
ska ersättas av ett logiskt uttryck eller variabel.
En villkorssats kan ha två förgreningar där man anger vad som ska utföras om ett villkor är sant och vad som annars ska utföras.
if <villkor>:
# indenterad kod som ska utföras om villkoret sant
else:
#indenterad kod som ska utföras om villkoret falsktTesta koden:
tal = int(input("Skriv ett heltal"))
if tal % 2 == 0:
print(tal, "är jämnt")
else:
print(tal, "är udda")Man kan hantera flera förgreningar med hjälp av ordet elif vilket är en förkortning av orden else if.
if <villkor1>:
# kod som ska utföras om villkor1 sant
elif <villkor2>:
# kod som ska utföras om villkor1 falskt men villkor2 sant
elif <villkor3>:
# kod som ska utföras om villkor1 och villkor2 falska men villkor3 sant
else:
# kod som ska utföras om alla villkor falskaEn if-sats kan innehålla godtyckligt många elif men endast ett else.
Testa koden:
ålder = int(input("Hur gammal är du?"))
if ålder < 18:
print("Du är omyndig.")
elif ålder < 65:
print("Du är i arbetsför ålder.")
else:
print("Du är pensionär")Om du vill generera slumptal i Python använder du funktioner som ligger i modulen random. Innan du kan använda slumptalsfunktionerna måste du skriva:
import randomFör att slumptalsgenerera ett heltal använder du funktionen random.randint(a, b), vilken returnerar ett heltal \(n\) sådant att \(a\le n \le b\).
För att generera ett flyttal \(x\) sådant att \(0 \le x \lt 1\) använder du funktionen random.random().
För att generera ett flyttal \(x\) sådant att \(a \le x \le b\) använder du funktionen random.uniform(a, b).
Lägg märke till att varje funktion skrivs med punktnotation efter random. Om du vill slippa använda punktnotation kan du istället för att skriva import random, skriva:
from random import randint, random, uniformTestkör denna kod upprepade gånger.
import random
a = random.randint(1, 10)
b = random.random()
c = random.uniform(2, 5)
print("a =", a)
print("b =", b)
print("c =", c)Ändra den översta raden så att punktnotation inte längre behövs.
Det finns flera funktioner i modulen random. Om dessa kan du läsa på sidan Python: Generate pseudo-random numbers.
I modulen math finns det fördefinierade funktioner och konstanter. Här finns exempelvis funktionen math.sqrt(a) vilken beräknar kvadratroten av \(a\) och funktionen math.gcd(a, b) vilken beräknar den största gemensamma delaren (greatest common divisor) av heltalen \(a\) och \(b\). I denna modul finns också ett närmevärde av konstanten \(\pi\) i math.pi.
För en fullständig lista av matematiska funktioner och konstanter se Python: Mathematical functions.
Om du vill använda modulen math måste du antingen skriva:
import mathoch sedan använda punktnotation, eller börja med att specificera vilka funktioner du vill använda genom att skriva:
from math import sqrt, gcd, piTesta koden:
from math import sqrt, pi
a = sqrt(5)
b = 5**0.5
print("a =", a)
print("b =", b)
print("pi =", pi)Testa att ta roten ur -1 genom att använda sqrt(-1) i tilldelningen till a.
Testa att göra tilldelningen b = (-1)**0.5.
Python har också en datatyp för komplexa tal. Den imaginära enheten skrivs med bokstaven j i Python. Modulen math hanterar bara reella tal och ger därför ett felmeddelande om man försöker ta roten ur -1. Det finns en annan modul cmath vilken hanterar komplexa tal.
Du kan definiera en egen funktion i Python och sedan använda den i koden. Att använda en funktion kallas för att anropa funktionen. När du anropar en funktion utförs den kod som finns i definitionen av funktionen.
En funktion kan returnera ett värde, som funktionerna i modulen math. Det går också att göra en funktion som inte returnerar ett värde utan bara utför ett stycke kod.
Definitionen av en funktion har följande struktur
def funktionsnam(<parameter1, parameter2, ...>):
# indenterad kod som ska utföras då funktionen anropasEventuella parametrar anges innanför parenteser efter funktionens namn. Flera parametrar åtskiljs av komma-tecken.
Om koden i definitionen innehåller ordet return följt av något värde, kommer detta värde att returneras.
Vi kan göra en funktion som adderar två tal och returnerar summan av talen.
def addera_tal(tal1, tal2):
return tal1 + tal2Funktionen har två parametrar tal1 och tal2. När vi anropar funktionen skickar vi in de värden parametrarna ska ha. Dessa värden kallas för funktionens argument.
Vi måste definiera funktionen innan den anropas.
def addera_tal(tal1, tal2):
return tal1 + tal2
a = int(input("a ="))
b = int(input("b ="))
summa = addera_tal(a, b)
print("summan =", summa)Det går också att skicka in funktionsanropet som ett argument till print().
print("summan =", addera_tal(a, b))konventionen inom Python är att funktionsnamn och variabelnamn som består av flera ord skrivs med små bokstäver med orden sepererade av understräck.
min_variabel
min_funktion()
Vi kan göra en funktion som skriver ut ett namn på en person och personens ålder.
def skriv_person(namn, ålder):
print("namn:", namn, " ålder:", ålder)
namn = input("Vad heter du? ")
ålder = int(input("Hur gammal är du? "))
skriv_person(namn, ålder)Variabler som är deklarerade inuti en funktion är så kallade lokala variabler.
Försök att lista ut vad utskriften blir med följande kod:
a = 10
b = -2
def min_funktion():
a = 5
lokal_variabel = 7
print("a = ", a)
print("b = ", b)
print("lokal_variabel = ", lokal_variabel)
min_funktion()
print("nu är a = ", a)Testkör sedan koden.
Prova att lägga till raden
print(lokal_variabel)längst ner i koden och teskör programmet igen.
När vi anropar funktionen
def skriv_person(namn, ålder):
print("namn:", namn, " ålder:", ålder)måste vi skriva argumenten i rätt ordning. Anropet
skriv_person("Emma", 16)fungerar. Anropet
skriv_person(16, "Emma")ger en felaktig utskrift.
Om vi inte vill bry oss om ordningen när vi skriver argumenten, kan vi skriva parameternamnet följt av ett värde när vi anropar funktionen. Anropet
skriv_person(ålder = 16, namn = "Emma")ger en korrekt utskrift. Ordningen spelar i detta fall ingen roll.
När du definierar en funktion kan de ge en eller flera parametrar förvalda värden. När en sådan funktion anropas behöver du inte ange alla argument.
Som exempel på en funktion med ett förvalt parametervärde kan vi använda Newtons andra lag vid fritt fall. Kraften är lika med massan gånger accelerationen. Vid ett fritt fall ges accelerationen av tyngdacceleration. Lagen kan skrivas som
\[F = mg\]där \(F\) är kraften, \(m\) massan och \(g\) tyngdaccelerationen. På jorden kan man räkna med att \(g = 9,8 \text{ m}/\text{s}^2\).
Vi kan göra en funktion
def F(m, g = 9.8):
return m*gmed ett förvalt värde på \(g\). Nu kan vi anropa funktionen med en parameter
print("Kraften är", F(60), "Newton.")om vi tänker oss att fallet är på jorden. Om vi tänker oss fritt fall på månen kan vi anropa funktionen med två parametrar:
print("Kraften är", F(60, 1.625), "Newton.")I och med att Python i så hög grad bygger på text, finns det flera olika sätt att formatera textsträngar.
Vi har tidigare sett hur man kan sätta samman textsträngar med variabelvärden genom att omvandla variabelvärden till textsträngar och sedan konkatenera.
a = 3
b = 7
svar = int(input("Vad är " + str(a) + "*" + str(b) + "?"))Vi kan åstadkomma samma textsträng inuti input() genom att istället använda så kallade f-strängar.
Vi kan formatera en textsträng genom att skriva bokstaven f framför textsträngen och sedan skriva variabelnamn innanför måsvingar.
a = 3
b = 7
svar = int(input(f"Vad är {a}*{b}?"))Det går bra att skriva uttryck innanför måsvingarna, som i koden:
a = 3
b = 7
print(f"{a}/{b} = {a/b}")Du kan välja att visa ett flyttal med två decimaler genom att skriva :.2f efter flyttalet innanför måsvingarna.
a = 3
b = 7
print(f"{a}/{b} = {a/b:.2f}")Vill du istället visa sex decimaler skriver du :.6f och så vidare.
I vanliga fall skrivs det ut ett minustecken framför negativa tal och inget tecken alls framför positiva tal. Du kan se till att ett tecken skrivs ut oavsett om talet är positivt eller negativt genom att skriva :+ efter talet innanför måsvingarna.
Gissa vilken utskrift följande kod ger:
a = -3
b = 7
c = -a/b
print(f"{a}")
print(f"{b}")
print(f"{b:+}")
print(f"{c:+}")
print(f"{c:+.2f}")Testkör sedan koden.
De programmeringsuppgifter (nedan) som handlar om att lösa ekvationer visar hur numerisk ekvationslösning kan programmeras. Med datoralgebraprogram, vilka också kallas CAS efter det engelska Computer Algebra System, kan man lösa ekvationer och i regel få lösningar som antingen beskrivs exakt (dvs med uttryck av heltal) eller approximativa lösningar (dvs som decimaltal).
Det Python-programmering i matematikundervisningen kan bidra med är en större förståelse för hur beräkningsmatematik fungerar, samt en förståelse för skillnaden mellan exakta lösningar och approximativa. Beräkningsmatematik används bl.a. för att programmera CAS. Denna förståelse är framför allt viktig för elever som går på matematikintensiva program på gymnasiet. Det är därför programmering är med i matematikämnet i gymnasiets C-spår men inte i övriga matematikkurser. För elever som inte studerar på matematikintensiva gymnasieprogram, är det kanske viktigare att de lär sig använda CAS än att de lär sig hur CAS programmeras.
Talet \(1/5\) är ett exakt tal men \(0,2\) är inte exakt. Utan användning av datorer är distinktionen mellan exakt och approximativ av filosofisk art. Om man stöter på talet \(0,2\) så vet man inte om det möjligen har blivit avrundat från \(0,20001\) eller om det är \(0,2000\ldots\) med oändligt många nollor i decimalutvecklingen, dvs exakt. Utan någon kontext måste man förutsätta att \(0,2\) inte är ett exakt tal, annars hade det skrivits som \(1/5\). Om datorer används är distinktionen mellan exakt och approximativ inte en fråga av filosofisk art. Flyttal har bara ett ändligt antal decimaler och kan inte ha en decimalutveckling med oändligt många nollor på slutet. När man använder flyttal blir det i regel avrundningsfel, avrundningsfel som efter upprepade beräkningar kan få konsekvenser.
Ett känt exempel på upprepade avrundningsfel som fick ödesdigra konsekvenser är uppskjutningen av en Patriot-missil under Gulfkriget år 1991. Missilen skulle träffa en inkommande irakisk scud-missil men räknade fel på scud-missilens bana. Felet uppkom som upprepade avrundningsfel. Som en konsekvens blev 28 soldater dödade av scud-missilen (se Wikipedia: MIM-104 Patriot; Failure at Dahhran).

Om du löser en ekvation med ett CAS-program kan du i regel ange om lösningen ska vara exakt eller approximativ. Med GeoGebras CAS kan du skriva in ekvationen
\[5x = 1\]och sedan välja hur lösningen ska visas genom att klicka på ett verktyg.
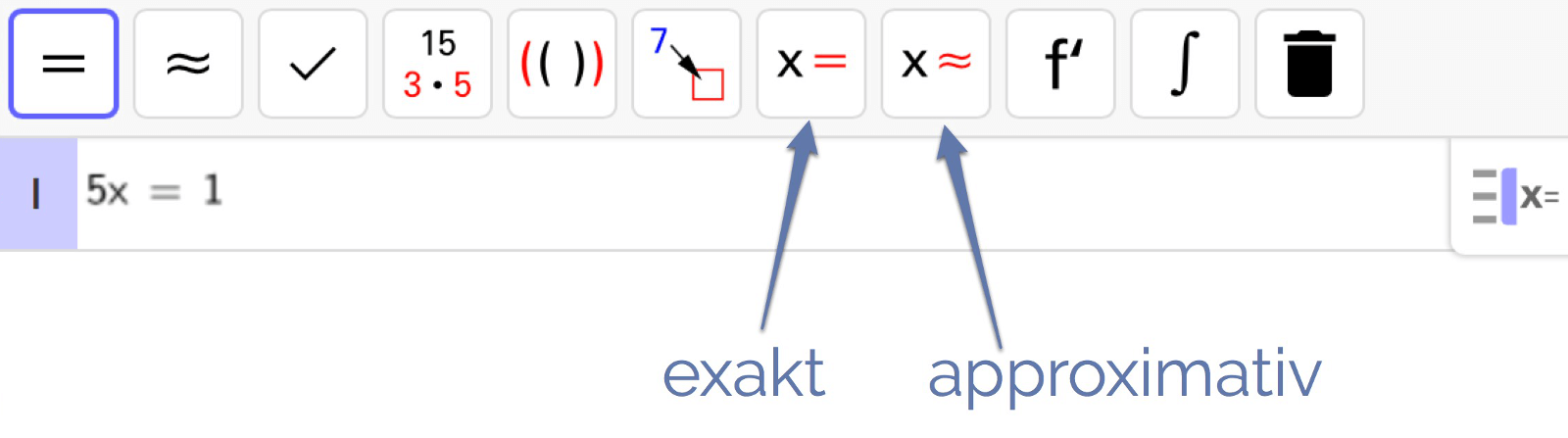
En exakt lösning skrivs som ett uttryck av heltal. En approximativ lösning skrivs som ett decimaltal. Testa på sidan https://www.geogebra.org/classic/cas!
Som en miniräknare
Använd Python Shell för att beräkna
0.55555555555555566414.142135623730951
Numeriska fel
Om du vill skriva talet \(1/7\) som ett decimaltal med ett visst antal decimaler är risken stor att du får ett avrundningsfel eftersom talet har oändligt många decimaler. Talet \(1/4\) däremot har en ändlig decimalutveckling och behöver därför inte avrundas (om man använder minst två decimaler).
När man gör numeriska beräkningar med en dator, används det binära talsystemet så eventuella avrundningsfel blir annorlunda än om man använder det decimala talsystemet.
Beräkna 0.1+0.2 samt 0.25+0.125 i Python Shell!
På vilket sätt skiljer sig resultaten åt? Kan du förklara skillnaden?
Vilken sorts rationella tal har en ändlig decimalutveckling när det decimala talsystemet används.
Vilken sorts rationella tal har en ändlig decimalutveckling när det binära talsystemet används.
Enhetsbyte
Gör ett program som tar emot en temperatur i grader Celsius som indata och sedan visar temperaturen i Fahrenheit. Formeln för konvertering är
\[F = \frac{9}{5}C+32. \]Kontrollera ditt program genom att testa om \(20\) grader Celsius blir \(68\) grader Fahrenheit.
Beräkna medelvärde
Gör ett program som först låter användaren mata in två tal, därefter ska medelvärdet av talen beräknas och skrivas ut. En körning av programmet kan se ut så här:
Tal 1: -2.3 Tal 2: 3.6 Medelvärdet är 0.6500000000000001
Andragradsekvation med två rötter
En andragradsekvation på formen
\[x^2+px+q=0\]kan lösas av den så kallade pq-formeln
\[x = -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q}.\]Gör ett program som först låter användaren mata in p och sedan q. Sedan ska programmet beräkna och skriva ut de två rötterna.
Ekvationen kan ha noll, en eller två rötter. Ditt program behöver bara klara fallet att ekvationen har två rötter. Exempelvis ska \(p=10\) och \(q=5\) ge rötterna -0.5278640450004204 och -9.47213595499958.
Spara ditt program. Vi ska senare korrigera koden.
Tid
Gör ett program som tar emot ett antal minuter som indata och sedan visar hur många timmar och minuter denna tid motsvarar.
Bankomat
Gör ett program som simulerar en bankomat. Låt användaren skriva in ett uttag. Visa sedan hur många hundra-, tvåhundra- och femhundra-lappar bankomaten ska mata ut.
Dividera tal
Öva multiplikation
Gör att program som ställer frågan "Vad är 7*8?" och sedan kontrollerar om svaret var rätt eller fel.
Se till att det två talen slumptalsgenereras så att det blir olika frågor varje gång programmet körs.
Godtycklig andragradsekvation
Vid lösningen av en andragradsekvation med pq-formeln kommer vissa värden på \(p\) och \(q\) ge ett uttryck innanför rotuttrycket som är negativt. Sådana ekvationer saknar reella lösningar. Uttrycket innanför rotuttrycket kallas för diskriminanten. Med andra ord är
\[\text{diskriminanten} = \left(\frac{p}{2}\right)^2-q.\]Korrigera ditt program för lösning av andragradsekvationer så att programmet skriver ut noll, en eller två rötter.
Gör en variabel för diskriminanten och använd sedan denna i en villkorssats.
Cirkels omkrets och area
Gör en funktion som beräknar en cirkels area och en funktion som beräknar en cirkels omkrets. Båda funktionerna ska ta emot radien som argument. Använd det närmevärde på \(\pi\) som finns i modulen math.
Låt användaren skriva in radien och visa sedan area och omkrets.
Temperaturomvandlingar
Gör ett program som låter användaren antingen omvandla från Celsius till Fahrenheit eller tvärtom.
Gör en funktion för vardera omvandling. Utgå ifrån formeln
\[ F = \frac{9}{5}C+32\]När programmet startar ska användaren få välja vilken omvandling som ska utföras.
1: Omvandla från Celsius till Fahrenheit 2: Omvandla från Fahrenheit till Celsius Vilken omvandling vill du göra? Skriv 1 eller 2:
När du kollar om svaret är ett eller två behöver du inte omvandla till heltal. Det går att jämföra textsträngar.
if val == "1":Låt sedan användaren ange en temperatur, utför den valda omvandlingen och visa resultatet på valfritt sätt.
Kontrollera ditt program genom att testa om 20 grader Celsius blir 68 grader Fahrenheit, och vice versa.
Lös enkel linjär ekvation
Gör ett program som löser den linjära ekvationen
\[ax+b = c\]där koefficienterna \(a\), \(b\) och \(c\) är tal som användaren matar in.
Om användaren matar in a = 0, b = 1 och c = 2 (dvs ekvationen \(1=2\)) ska programmet visa utskriften
Ekvationen 1 = 2 saknar lösning.
eftersom denna likhet inte är sann för något värde på \(x\). Vad är det som ska gälla i det allmänna fallet för att ekvationen ska sakna lösning?
Om användaren matar in a = 0, b = 1 och c = 1 (dvs ekvationen \(1=1\)) ska programmet visa utskriften
Ekvationen 1 = 1 har oändligt många lösningar.
eftersom denna likhet är sann för alla värden på \(x\). Vad är det som ska gälla i det allmänna fallet för att ekvationen ska ha oändligt många lösningar?
Om användaren matar in koefficienter som ger precis en lösning ska denna lösning visas.
Lös svårare linjär ekvation
Gör ett program som löser den linjära ekvationen
\[ax+b = cx + d\]där koefficienterna \(a\), \(b\), \(c\) och \(d\) är tal som användaren matar in.
Se till att programmet visar korrekta utskrifter oavsett om ekvationen har noll, en eller oändligt många lösningar.
Öva ekvationslösning
Gör ett program som visar en ekvation och frågar efter lösningen.
Lös ekvationen 3x+5=23 Vad är x?
De tre koefficienterna \(a\), \(b\) och \(c\) i ekvationen
\[ax+b = c\]ska vara slumpade heltal sådana att \(a \ne 0\). För enkelhetens skull kan du se till att \(a \ge 2\). Roten \(x\) ska också vara ett heltal.
Slumpa fram tre av heltalen och beräkna det fjärde heltalet. I vilken ordning ska detta göras för att ekvationen garanterat ska ha en heltalslösning?
Om koefficienten \(b\) är negativ ska ekvationen visas på följande sätt:
Lös ekvationen 3x-5=23
Se Exempel 12 för kod som formaterar tal med tecken.
När användaren besvarat frågan ska du visa "rätt" eller "fel" på valfritt sätt.