

As a novice, you will not learn programming by merely reading or listening. Using this teaching material, you are expected to run the examples while reading the text. The examples are short and often made so you can copy some code, paste it into an editor, and then make some minor change.
For a full reference of the Python language, see Python 3.6.7 documentation. At that site you can choose version in the upper left corner.
Start by making an account on https://repl.it. Then click Start coding now. Choose Python in the list that appears. Your Python program is created.
Write the code:
print("Welcome!")in the editor (the middle window) and then click on the green arrow to run the code. The output is shown in the black window to the right.
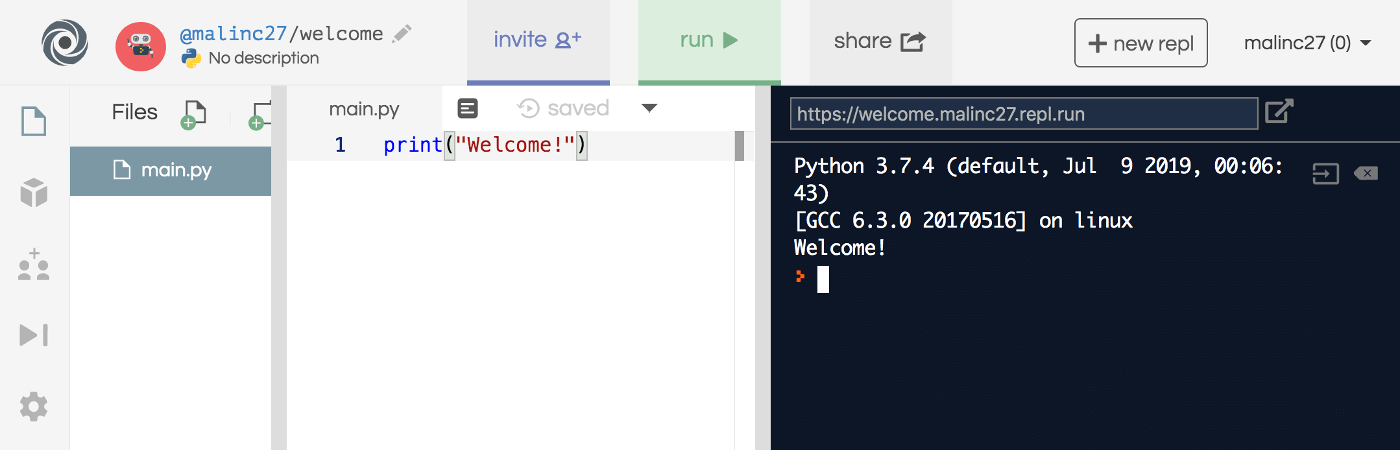
If you want to make a new program, click on + new repl .
The black console to the right is not only used for showing output from programs. In the console a program called Python Shell is run, which makes the console interactive. You can write code in the console and then run it. Python Shell sees to it that the Python interpreter interprets the code to executable code, and then runs the code. After that any possible output is shown.
An environment like Python Shell can be called REPL which stands for Read Eval Print Loop.
You can use Python Shell as a calculator. The arithmetic operators in Python are:
| operator | operation | example | result |
|---|---|---|---|
+ - * / |
make a guess! | 4.3+2.7 |
7.0 |
** |
to the power of | 2**3 |
8 |
% |
remainder | 20%6 |
2 |
// |
quotient | 20//6 |
3 |
Precedence of arithmetic operators:
The calculation 15-6*2 yields the result 3.
The calculation (15-6)*2 yields the result 18.
Calculate 2*3**2 in Python Shell. Which of the operators * and ** is used first?
Variables are used for storing values used by the program. A variable has a name and a value.
You make a variable by writing a variable name and then assigning it a value using the equality symbol. The equality symbol does not denote an equality but an assignment.
Write a = 7 and press enter. Then write a to see the value of the variable.
Repeatedly write a = a + 1 and press enter. Then show the value of the variable a.
By using the up and down arrow keys, you can step through all commands you have written in the Python Shell. This is handy when you want to execute some code over and over again.
The statement a = a + 1 is an assignment that works since the value of the expression to the right of the equality symbol is first found, then this value is assigned to a.
When you assign a value to a variable, that value is of some data type. Since everything is represented by binary numbers internally, there must be a way to know how to interpret a sequence of binary digits. Do the binary digits represent an integer, or a decimal number, or something else? Depending on the data type, the Python interpreter will know how to interpret various sequences of binary digits. When you assign a value to a variable, Python finds the suitable data type. You can use the function type() to find the data type of a variable.
Make the three variables a = 15, b = 2.7 and c = "Hello!" in Python Shell.
Then write type(a), type(b) and type(c).
In Python you can change the data type of a variable by assigning it a new value. Try writing a = "Huh?" and then type(a).
The data type int stands for integer.
The data type float stands for floating point. Floating point is the data type used for decimal numbers. Unlike a decimal number, a floating point always has a finite number of decimals.
The data type str stands for string. Strings are used for storing text.
Apart from these three data types there is also a data type called bool, which stands for Boolean. The Boolean data type is used for logical values, i.e. values that are either true or false. The Boolean data type is named after George Boole who invented the so-called Boolean algebra.
A Boolean value in Python is either True or False.
The Boolean operators (also called logical operators) in Python are: and, or, and not.
A Boolean operator operates on Boolean values and the result is a Boolean value.
A comparison operator operates on numerical values and the result is a Boolean value. The comparison operators in Python are:
| operator | comparison |
|---|---|
== |
equal med |
!= |
not equal to |
< |
less than |
<= |
less than or equal to |
> |
greater than |
>= |
greater than or equal to |
Since a single equality sign is used for assignment, double equality signs are used for equality.
Make some variables using Boolean values and Boolean expressions in Python Shell.
a = 5 < 7,
b = False,
a and b,
not b,
a or 3*4 >= 12,
c = 0 < 5 < 10.
A string is either enclosed by double quotation marks (") or single quotation marks (').
a = "Hello"
b = 'Some text with blanks.'
c = '3'
If you need a string that contains a single quotation mark, you can use double quotation marks, and vice versa.
Make a variable a that has the value: "Eureka" he shouted.
Make a variable b that has the value:
It's called Archimedes' principle.
Try writing 3*a.
Try writing 3+a.
Try writing a+b.
Try writing a*b.
Using Python Shell can be convenient in some cases but in general you will use the editor to make programs. From now on we will use the editor and run the code by pressing the green arrow.
When you write code in the editor, you show output by using the print() function. The function print() can take several arguments separated by a comma.
The code:
a = 7
b = 13
print("a = ", a)
print("b = ", b)
print("the sum is", a+b)Yields the output:
a = 7 b = 13 the sum is 20
The function print() ends a print by making a new line. You can choose another way to end by specifying the argument end, this argument could be set to a blank, or something else. There is also an argument sep that can be used for separating the output of the arguments. By default, they are separated by a blank but you can choose something else.
The code:
a = 7
b = 13
print("a = ", a, end = " ")
print("b = ", b)
print("the sum is", a+b, sep ="")Yields the output:
a = 7 b = 13 the sum is20
Can you see the difference between the two outputs?
To receive input from the user you use the function input(). As argument to this function, you write a string that will be shown in the console. The function input() returns whatever the user has written as a string. The answer can be saved as the value of a variable, as in the code:
name = input("What's your name?")
print("Hi", name)If you want the user to enter numerical values to be used in numerical expressions, you must convert the string to a numerical data type. Converting data types like this is called type casting. There are several built-in functions in Python for type casting.
int() converts to an integer.float() converts to a floating number.str() converts to a string.There is a list of type built-in functions at Python: Built-in Functions.
Try out the code:
# Add two integers.
astr = input("a =") #get input as a string
bstr = input("b =")
a = int(astr) #convert it to integer
b = int(bstr)
the_sum = a+b
print("a+b =",the_sum)Then change to code to:
# Add two integers.
a = int(input("a =")) #get input and convert it to integer
b = int(input("b ="))
the_sum = a+b
print("a+b =",the_sum)Whatever is written after # is a so-called comment. Comments are not executed but may be helpful for the person reading the code.
Change the code so two floating point numbers are added instead of two integers.
The function print() automatically converts all arguments to strings. The function input() on the other hand, only takes one argument which must be a string.
If you want to combine some text that you write as a string in the code, with the value of a variable, you must first convert the value of the variable to string, then you combine string values using the operator +. Combining strings like this is called concatenating.
a = 3
b = 7
answ = int(input("What is " + str(a) + "*" + str(b) + "?"))In order to ask a question like this and then let the program tell the user whether the answer was correct or not, we will need a so-called conditional statement.
A conditional statement is used to let the program do different things depending on some condition. The most common conditional statement in most programming languages is an if statement.
A simple if statement in Python is written like this:
if <condition>:
# indented code to be executed if the condition is trueThe code to be executed if the condition is true, must be indented, i.e. it must be preceded by whitespace that can either be some blanks or a tab. The editor used by repl.it will automatically indent when you press enter after the colon. All indented code following the colon will be executed if the condition is true.
Placeholders in code examples
The pink text starting with < and ending with > is a so-called placeholder. The placeholder must be replaced by a variable or an expression. The placeholder
<condition>
should be replaced by a logical expression or a Boolean variable.
A conditional statement can have two branches.
if <condition>:
# indented code to be executed if the condition is true
else:
# indented code to be executed if the condition is falseTry out the code:
n = int(input("Write an integer"))
if n % 2 == 0:
print(n, "is even")
else:
print(n, "is odd")You can make several branches by using the word elif which is a short form of else if.
if <condition1>:
# code to be executed if condition1 is true
elif <condition2>:
# code to be executed if condition1 is false but condition2 is true
elif <condition3>:
# code to be executed if condition1 and condition2 are false
# but condition3 is true
else:
# code to be executed if all conditions are falseAn if statement can have any number of elifs but at most one else.
Try out the code:
age = int(input("How old are you?"))
if age < 18:
print("You are a child.")
elif age < 65:
print("You are an adult.")
else:
print("You may retire.")When you want to generate random numbers in Python, you use functions from the module random. Before you can use these functions, you must import the module by writing:
import randomTo generate a random integer you use the function random.randint(a, b) that generates an integer \(n\) such that
\(a\le n \le b\).
To generate a floating number \(x\) such that \(0 \le x \lt 1\) you use the function random.random().
To generate a floating number \(x\) such that \(a \le x \le b\) you use the function random.uniform(a, b).
Note that each function is written using dot notation after random. If you don't want to use dot notation, you can do the import in another way. Instead of writing import random, you write:
from random import randint, random, uniformTry running this code several times.
import random
a = random.randint(1, 10)
b = random.random()
c = random.uniform(2, 5)
print("a =", a)
print("b =", b)
print("c =", c)Change the code so you don't need dot notation
There are several functions in the module random. For more information see: Python: Generate pseudo-random numbers.
In the module math some mathematical functions and constants are defined. As an example there is a function math.sqrt(a) that calculates the square root of \(a\), and a function math.gcd(a, b) that returns the greatest common divisor of integers \(a\) and \(b\). This module also has an an approximation of \(\pi\) in the constant math.pi.
For a full list of functions and constants see: Python: Mathematical functions.
If you want to use the module math you can either write:
import mathand then use dot notation, or specify what functions or constants you need by writing:
from math import sqrt, gcd, piTry out the code:
from math import sqrt, pi
a = sqrt(5)
b = 5**0.5
print("a =", a)
print("b =", b)
print("pi =", pi)Try finding the square root of -1 by using sqrt(-1) in the assignment of a.
Try making the assignment b = (-1)**0.5.
Python also has a data type for complex numbers. An imaginary number is written using j as a suffix to the imaginary part. The module math can only handle real numbers. There is another module cmath that only handles complex numbers. The module numpy can handle both real and imaginary numbers, and addition to this, numpy has lots of functionality for more advanced mathematics.
We have seen that there are some predefined functions in Python, such as print(), and some functions that are defined in modules. You can also define a function yourself and then use it by calling it. When you call a function, the code written in its definition is run.
A function can return a value, as the functions in the module math or the input() function. A function can also just do something, without returning a value, like the function print().
The definition of a function has following structure:
def function_name(<parameter1, parameter2, ...>):
# indented code that is run when the function is calledIf the function has parameters, they are written between the parentheses after the function name. Several parameters are separated by comma signs. If the function doesn't have any parameters, you must still write the parentheses.
# a function without parameters
def function_name():
# indented code that is run when the function is calledIf the code in the definition has the word return, followed by some value, then that value will be returned.
We can make a function that adds two numbers and returns the sum.
def add_numbers(number1, number2):
return number1 + number2The function has two parameters number1 and number2. When we call the function, we must specify values for the parameters. These values are called the arguments of the function.
We must define a function before we call it.
def add_numbers(number1, number2):
return number1 + number2
a = int(input("a ="))
b = int(input("b ="))
the_sum = add_numbers(a, b)
print("sum =", the_sum)The function call can also be used as argument to print().
print("sum =", add_numbers(a, b))by convention, names in Python that contain several words are separated by underscore.
my_variable
my_function()
We can make a function that prints the name and age of a person.
def print_person(name, age):
print("name:", name, " age:", age)
name = input("What's your name? ")
age = int(input("How old are you? "))
print_person(name, age)Variables that are made inside the definition of a function are so-called local variables.
Guess the output of this code:
a = 10
b = -2
def my_function():
a = 5
local_variable = 7
print("a = ", a)
print("b = ", b)
print("local_variable = ", local_variable)
my_function()
print("now a = ", a)Then run the code.
Add this row
print(local_variable)at the bottom of the program. Then run the program once more.
When we call the function
def print_person(name, age):
print("name:", name, " age:", age)we must pass the arguments in the same order as in the definition; the name comes first, then the age. The function call
print_person("Emma", 16)works, whereas the call
print_person(16, "Emma")doesn't work.
By naming the arguments in the function call, we can use any ordering we want. The position of an argument is no longer needed to determine what parameter value it should be, that is given by the name in the function call. The call
print_person(age = 16, name = "Emma")works.
When calling a function, you can first pass a number of positional arguments (you only use the values), and then a number of keyword arguments (arguments preceded by the name of corresponding parameter).
The function
def print_person(name, age, country):
print("name:", name)
print("age", age)
print("country:", country)can be called like this:
print_person("Emma", country="Sweden", age=16)The argument "Emma" must be the value given to the parameter name, due to its position. The two keyword arguments can be in any order within the function call.
When you define a function, you can give default values to one or several parameters. When you call a function with default parameter values, you don't have to pass all arguments. We have seen this with the built-in function print(), we don't have to pass values for sep or end since they have default values.
As an example of a function with a default parameter value, we can use Newton's second law of motion, for falling objects: the force is the mass times the acceleration. If an object is dropped on earth, the acceleration is constant and can be written as
\[F = mg\]where \(F\) is the force, \(m\) the mass and \(g\) is the constant acceleration due to gravity. On earth we can use \(g = 9,8 \text{ m}/\text{s}^2\).
We can make the function
def F(m, g = 9.8):
return m*gusing a default value for \(g\). Now we can call the function with one argument
print("The force is", F(60), "Newton.")if the fall is on earth. If an object is falling on the moon, we can call the function using two arguments:
print("The force is", F(60, 1.625), "Newton.")Since Python is often used for text-based programs, there are several ways to format a string.
We have previously seen that we can concatenate strings using the + operator.
a = 3
b = 7
answ = int(input("What is " + str(a) + "*" + str(b) + "?"))We can produce the same string as an argument to input() by instead using a so-called f-string.
We can format a string by using the letter f as a prefix to the string, and then write variable names within curly brackets.
a = 3
b = 7
answ = int(input(f"What is {a}*{b}?"))You can write expressions within the curly brackets, as in the code:
a = 3
b = 7
print(f"{a}/{b} = {a/b}")You can show two decimals of a floating point number by writing :.2f after the number inside the curly brackets.
a = 3
b = 7
print(f"{a}/{b} = {a/b:.2f}")If you want to show six decimals, you write :.6f, etc.
By default, a minus sign is written in front of negative numbers, and no sign in front of positive. You can see to it that a sign is always written by writing :+ after the number inside the curly brackets.
Guess the ouput of this code:
a = -3
b = 7
c = -a/b
print(f"{a}")
print(f"{b}")
print(f"{b:+}")
print(f"{c:+}")
print(f"{c:+.2f}")Then run the code.
The exercises below about solving equations, are examples of how numerical equation solving can be done. With CAS (Computer Algebra System) programs, you can solve equations and choose whether you want an exact solution (expressed using integers) or a numerical approximation of the solution (a floating point).
The number \(1/5\) is an exact number whereas \(0,2\) is an approximation. When not using a computer, the distinction between exact and approximation is a matter that you can discuss, a philosophical distinction. If you see the number \(0.2\), without any context, you don't know if it has been rounded from \(0,20001\) (approximation) or if it is \(0,2000\ldots\) with infinitely many zeros in the decimal expansion (exact). Without any context you must assume it is an approximation, otherwise it would have been written as \(1/5\). When a computer is used, the distinction between exact and approximation is not a philosophical distinction. Floating point numbers have a finite number of decimals and cannot have infinitely many zeroes in the decimal expansion. When you use floating numbers, you will often get rounding errors. Repeated rounding errors may have surprising, and unwanted, outcomes.
A known example of repeated rounding errors that had severe consequences, is the launch of a Patriot-missile during the Gulf war in 1991. The missile should supposedly hit an incoming Iraqi scud missile, but the calculation of the trajectory of the scud missile was not correct, due to repeated rounding errors. As a consequence, 28 soldiers were killed by the scud missile (see Wikipedia: MIM-104 Patriot; Failure at Dahhran).

If you solve an equation using some CAS program, you can often choose whether you want an exact solution or an approximation. Using the CAS of GeoGebra, you can write the equation
\[5x = 1\]and then choose how to display the solution by choosing one of two tools.

An exact solution is displayed using an expression of integers. An approximative solution is displayed as a decimal number. Check it out at: https://www.geogebra.org/classic/cas!
As a calculator
Use Python Shell to calculate
0.55555555555555566414.142135623730951
Numerical rounding errors
If you write \(1/7\) as a decimal number with some given number of decimals, you may get a rounding error since the number has infinitely many non-zero decimals. The number \(1/4\), on the other hand, has a finite decimal expansion and hence you will get no rounding errors (assuming you use at least two decimals).
When you do numerical calculations using a computer, binary numbers are used. For that reason, possible rounding errors occur for other numbers.
Calculate 0.1+0.2 and 0.25+0.125 in Python Shell!
What's the difference between the results? Can you explain this?
What rational numbers have a finite decimal expansion when the decimal number system is used?
What rational numbers have a finite decimal expansion when the binary number system is used?
Converting units
Make a program that takes a temperature in Celsius as input and shows the temperature in Fahrenheit. The formula for the conversion is
\[F = \frac{9}{5}C+32. \]Use the equality \(20 ^{\circ}C= 68^{\circ}F\) to check out your program.
Find the mean value
Make a program that lets the user enter two numbers, then it calculates the mean value of the numbers and shows the result. Running the program may look like this:
Number 1: -2.3 Number 2: 3.6 The mean value is 0.6500000000000001
Quadratic equations with two real roots
A quadratic equation of the form
\[ax^2+bx+c=0\]can be solved by the quadratic formula
\[x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]Make a program that first lets the user enter values for \(a, b\) and \(c\). Then the program should calculate and show the roots.
The equation can have zero, one, or two real roots. Your program only needs to handle the case of two real roots. As an example \(a = 1, b=10\) and \(c=5\), should yield the roots -0.5278640450004204 and -9.47213595499958.
Save your program. We will later refine the code.
Time units
Make a program that takes a number of minutes as input and then shows how many hours and minutes this corresponds to.
Automatic teller machine
Make a program that simulates an automatic teller machine. Let the user enter a cash withdrawal. Then show how many bills of various denomination values the machine will give the user.
Divide numbers
Practice multiplication
Make a program that asks "What is 7*8?" and then checks if the answer is correct or not.
See to it that the two numbers are randomly generated each time the program is run.
A general quadratic equation
A general quadratic equation may not have any real roots. When using the quadratic formula to solve a quadratic equation, you get an expression inside the square root. When this expression is negative, the equation has no real roots. Using the discriminant \(D = b^2-4ac\), it is easy to tell how many real roots a quadratic equation has.
Change your program for solving quadratic equations so the program outputs the number of real roots.
Make a variable for the discriminant and use it in a conditional statement.
Circumference and area of a circle
Make a function that calculates the area of a circle and a function that calculates the circumference. Both functions should have a parameter for the radius. Use the value of \(\pi\) given by the constant in the module math.
Let the user enter the value of the radius, then show the area and the circumference.
Convert units for temperature
Make a program that lets the user convert from Celsius to Fahrenheit, or the other way around.
Make a function for each of the two conversions. Use the formula
\[ F = \frac{9}{5}C+32.\]When the program starts, the user is given a choice:
1: Convert from Celsius to Fahrenheit 2: Convert from Fahrenheit to Celsius What conversion do you want to use? Write 1 or 2:
When you check the answer, you don't have to cast to an integer. It is possible to compare strings.
if choice == "1":Then let the user input a temperature, do the conversion and print the result.
Verify that your program converts \(20^{\circ}C\) to \(68^{\circ}F\), and vice versa.
Solve a simple linear equation
Make a program that solves the linear equation
\[ax+b = c,\]where the coefficients \(a\), \(b\) and \(c\) are numbers that the user inputs.
If the user inputs a = 0, b = 1 and c = 2 (the equation \(1=2\)), the program should show the output
The equation 1 = 2 has no solution.
since this equality isn't true for any value of \(x\). In the general case, for what values of the coefficients does the equation have no solution?
If the user enters a = 0, b = 1 and c = 1 (the equation \(1=1\)), the program should show the output
The equation 1 = 1 has infinitely many solutions.
since this equality is true for all values of \(x\). In the general case, for what values of the coefficients does the equation have infinitely many solutions?
If the user inputs values for an equation that has exactly one solution, this solution should be calculated and shown.
Solve a more difficult linear equation
Make a program that solves the equation
\[ax+b = cx + d,\]where \(a\), \(b\), \(c\) and \(d\) are numbers that the user inputs.
See to it that the program displays correct output regardless if the equation has zero, one or infinitely many solutions.
Practice solving equations
Make a program that shows an equation and asks for its solution.
Solve the equation 3x+5=23 What is x?
The three coefficients \(a\), \(b\) and \(c\) in the equation
\[ax+b = c\]should be random generated integers such that \(a \ne 0\). For simplicity, let \(a \ge 2\). The root \(x\) should also be an integer.
Generate three of the integers and calculate the fourth integer. In what order should you do this to ensure that the equation has an integer solution?
If the coefficient \(b\) is negative, the equation should be shown in the following way:
Solve the equation 3x-5=23
See Example 12 for code that formats the sign of a number.
When the user has answered the question, you can give some sort of feedback of your own choice.