

Det finns tre transformationer i Processing: translation, rotation och skalning. Dessa behövs framför allt om man vill rotera en bild eller visa den som spegelvänd.
När man ritar upp någonting i Processing, antingen något som ritas med hjälp av kod eller en bild från en bildfil, anger man bildens position genom att ange koordinater. Man kan därför undra varför translationer behövs. Vill man flytta på en uppritad bild kan man bara ange ny position för bilden. Translationer behövs framför allt om man vill rotera en bild. När en bild roteras gör den det runt en punkt. I Processing sker alla rotationer runt origo, vilken ligger i det övre vänstra hörnet av ritområdet. Vill man rotera runt någon annan punkt, gör man det genom att flytta hela koordinatsystemet. En translation gör just detta, den flyttar hela koordinatsystemet.
Funktionen
translate(<x>, <y>);flyttar det koordinatsystem som används vid utritning så att origo hamnar i punkten (<x>, <y>).
Med koden
function setup() {
createCanvas(windowWidth, windowHeight);
background(100);
}
function draw() {
rect(0, 0, 200, 100);
}ritas en rektangel med det övre vänstra hörnet i origo. Om man ändrar koden i draw-funktionen till
function draw() {
translate(200, 100);
rect(0, 0, 200, 100);
}kommer koordinatsystemet att flyttas till positionen (200, 100), därefter ritas rektangeln relativt det flyttade koordinatsystem och hamnar med det övre vänstra hörnet i punkten (200, 100) relativt det ursprungliga koordinatsystemet.
Om vi använder funktionen translate() igen inuti draw-funktionen, kommer nästa förflyttning av koordinatsystemet att utföras relativt föregående koordinatsystem. Tre på varandra följande translationer, som i koden
function draw() {
translate(200, 100);
rect(0, 0, 200, 100);
translate(200, 100);
rect(0, 0, 200, 100);
translate(200, 100);
rect(0, 0, 200, 100);
}ritar upp följande bild.
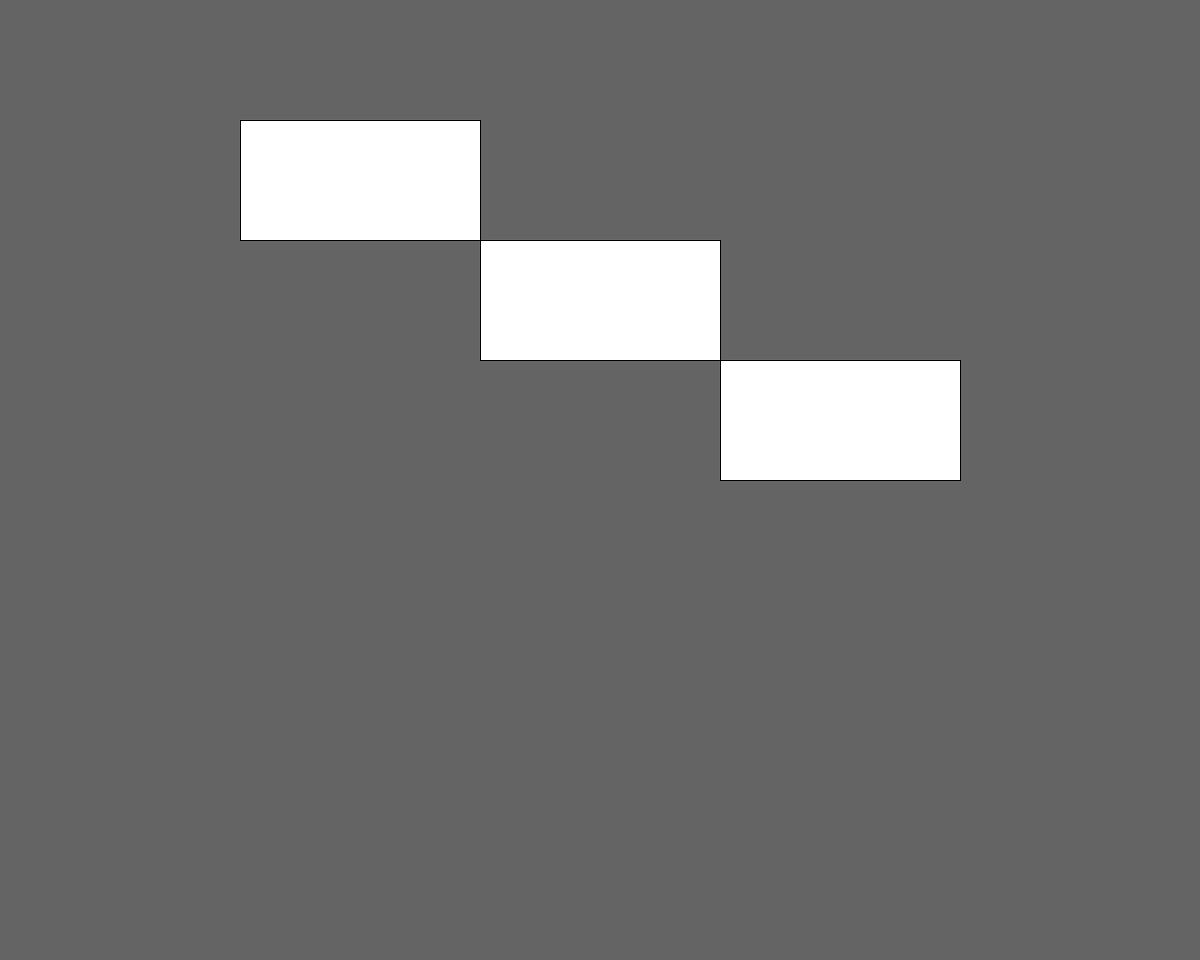
För att återställa koordinatsystemet kan man göra funktionsanropet
resetMatrix();Om vi vill rita upp samma bild men också anropa funktionen resetMatrix() efter den andra rektangeln, måste den tredje translationen vara relativt det ursprungliga koordinatsystemet, dvs:
function draw() {
translate(200, 100);
rect(0, 0, 200, 100);
translate(200, 100);
rect(0, 0, 200, 100);
resetMatrix();
translate(600, 300); // relativt ursprungligt koordinatsystem
rect(0, 0, 200, 100);
}Funktionen för att återställa koordinatsystem heter resetMatrix() efterom så kallade matriser används för alla transformationer (se Wkipedia: Matris).
Varje gång draw-funktionen ska genomlöpas återställs alla transformationer, man behöver alltså inte anropa resetMatrix() i början av draw-funktionen.
Translationer kan vara användbara om man vill rita bilder genom att skriva kod. Man kan definiera hur bilden ska ritas upp genom att anta att origo ligger i mitten av bilden, vilket är enklare än att rita relativt en position \( (x, y ) \). Innan bilden ritas, translaterar man koordinatsystemet till den position där bilden ska ritas.
Bilder som ritas med kod kan ibland vara enklare att beskriva om origo befinner sig i mitten av bilden, som i koden:
function setup() {
createCanvas(windowWidth, windowHeight);
rectMode(CENTER);
noStroke();
}
function draw() {
background(100);
translate(mouseX, mouseY);
bild();
}
function bild() {
fill(255, 0, 0);
ellipse(-40, 0, 20, 40);
ellipse(40, 0, 20, 40)
ellipse(0, -40, 40, 20)
ellipse(0, 40, 40, 20)
fill(255);
rect(0, 0, 60, 60);
}Testkör koden. Ändra i koden så att bilden ritas upp i mitten av ritområdet, inte där muspekaren befinner sig.
En rotation sker alltid runt någon punkt. I Processing utförs alla rotationer runt origo. För att rotera koordinatsystemet använder man funktionen
rotate(<vinkel>);Positiva vinklar ger rotation i medurs riktning.
Rotationer i Processing använder sig av vinkelenheten radianer såvida man inte använder kommandot angleMode(DEGREES). För att rotera en rektangel 30 grader runt origo, kan man använda koden:
function setup() {
createCanvas(windowWidth, windowHeight);
angleMode(DEGREES);
background(100);
}
function draw() {
rotate(30);
rect(200, 100, 200, 100);
}Genom att öka vinkeln varje gång draw-funktionen genomlöps, kan man se hur rektangeln roterar runt origo.
var vinkel;
function setup() {
createCanvas(windowWidth, windowHeight);
angleMode(DEGREES);
background(100);
vinkel = 0;
}
function draw() {
rotate(vinkel);
rect(200, 100, 200, 100);
vinkel += 5;
}Om man vill rotera en rektangel runt någon punkt, börjar man med att flytta koordinatsystemet till denna punkt. Därefter roterar man. När rektangeln ritas upp ska den ritas relativt origo, eftersom man flyttat origo.
function setup() {
createCanvas(windowWidth, windowHeight);
angleMode(DEGREES);
background(100);
}
function draw() {
rect(200, 100, 200, 100);
translate(200, 100);
rotate(30);
rect(0, 0, 200, 100); // ritas relativt origo
}Genom att öka vinkeln varje gång draw-funktionen genomlöps, kan man se hur rektangeln roterar runt punkten.
var vinkel;
function setup() {
createCanvas(windowWidth, windowHeight);
angleMode(DEGREES);
background(100);
vinkel = 0;
}
function draw() {
translate(200, 100);
rotate(vinkel);
rect(0, 0, 200, 100);
vinkel += 5;
}Om man vill rotera en rektangel runt sin egen mittpunkt, kan man se till att den ritas upp centrererad med kommandot rectMode(CENTER).
Om man vill ha två roterande objekt som roterar kring varsin punkt i motsatta riktningar, är det enklast att först skriva kod för den ena sammansatta transformationen och sedan återställa koordinatsystemet med kommandot resetMatrix(), därefter skriva kod för den andra sammansatta transformationen.
Två kvadrater roterar runt varsin punkt i motsatta riktningar.
var vinkel;
function setup() {
createCanvas(windowWidth, windowHeight);
background(100);
rectMode(CENTER);
angleMode(DEGREES);
vinkel = 0;
}
function draw() {
translate(width*0.3, height*0.3);
rotate(vinkel);
rect(0, 0, 200, 200);
resetMatrix();
translate(width*0.7, height*0.7);
rotate(-vinkel);
rect(0, 0, 200, 200);
vinkel += 5;
}Testkör koden. Se till att texten "MEDURS" visas mitt på den vänstra rektangeln och texten "MOTURS" mitt på den högra. För att centrera texten verktikalt och horisontellt kan du skriva
textAlign(CENTER, CENTER);i setup-funktionen. Sätt också textens storlek med textSize(<storlek>).
Tänk på att både texterna ska placeras i origo eftersom koordinatsystemet är förflyttat.
Genom att successivt förflytta och rotera ett objekt kan man få en roterande rörelse framåt.
Bilden förflyttas och roteras.
var x, y, deltax, deltay, vinkel;
function setup() {
createCanvas(windowWidth, windowHeight);
background(0);
noStroke();
rectMode(CENTER);
angleMode(DEGREES);
x = 100;
y = 100;
deltax = 5;
deltay = 3;
vinkel = 0;
}
function draw() {
background(0);
translate(x, y);
rotate(vinkel);
bild();
x += deltax;
y += deltay;
vinkel += 5;
}
function bild() {
fill(255, 0, 0);
ellipse(-40, 0, 20, 40);
ellipse(40, 0, 20, 40)
ellipse(0, -40, 40, 20)
ellipse(0, 40, 40, 20)
fill(255);
rect(0, 0, 60, 60);
}Istället för att helt rita över bakgrunden i draw-funktionen kan man rita över med en halvgenomskinlig färg. Byt den första raden i draw-funktionen till:
background(0, 10);Funktionen scale() kan användas med en eller två argument. Med ett argument
scale(<skalfaktor>);används samma skalfaktor i \(x\)- och \(y\)-led. Med två argument kan man använda olika skalfaktorer i \(x\)- och \(y\)-led.
scale(<skalfaktorX>, <skalfaktorY>);Skalningen utgår alltid ifrån origo vilken innebär att origo är den enda punkt som inte förändras.
Med koden
function setup() {
createCanvas(400, 300);
background(100);
}
function draw() {
fill(255);
ellipse(width/2, height/2, 100);
scale(0.5, 1.5)
fill(255, 0, 0)
ellipse(width/2, height/2, 100);
}kommer den röda ellipsen att skalas om, dessutom förflyttas mittpunkten till hälften av width/2 och 1,5 gånger height/2. Den bild som ritas upp ser ur så här:

Om man vill skala om en figur utan att förflytta dess mittpunkt, kan man börja med att translatera till mittpunkten, därefter skala om, sist ritas figuren relativt origo. Om vi ändrar koden i draw-funktionen till:
function draw() {
fill(255);
ellipse(width/2, height/2, 200);
translate(width/2, height/2);
scale(0.5, 1.5)
fill(255, 0, 0)
ellipse(0, 0, 200); // relativt origo
}blir den uppritade bilden istället så här:

Det finns ingen funktion för att spegla en funktion, däremot kan man använda funktionen scale() med en skalfaktor som är -1 i \(x\)- eller \(y\)-led. Om skalfaktorn är -1 i \(x\)-led blir det en spegling i \(y\)-axeln, om skalfaktorn är -1 i \(y\)-led blir det en spegling i \(x\)-axeln.
För att spegla i en vertikal eller horisontell linje som går genom någon punkt som inte är origo, måste man translatera till punkten innan man skalar.
Det andra huset är spegelvänt med en vertikal symmetrilinje mitt igenom huset.
function setup() {
createCanvas(windowWidth, windowHeight);
textAlign(CENTER, CENTER);
textSize(30);
noStroke();
}
function draw() {
background(100);
translate(100, 200);
hus(1);
resetMatrix();
translate(300, 200);
scale(-1, 1);
hus(2);
}
function hus(nr) {
fill(50, 50, 250);
rect(-80, -100, 160, 100);
fill(250, 50, 50);
triangle(-100, -100, 0, -200, 100, -100);
fill(50, 250, 50);
rect(0, -90, 50, 90);
rect(-60, -80, 40, 40);
fill(0);
text("hus " + nr, 0, -130)
}Kopiera de fyra sista raderna i draw-funktionen. Rita ett hus nr 3 med skalfaktorerna (1, -1).
Rita upp ett hus nr 4 med skalfaktorerna (-1, -1) på positionen (500, 200).
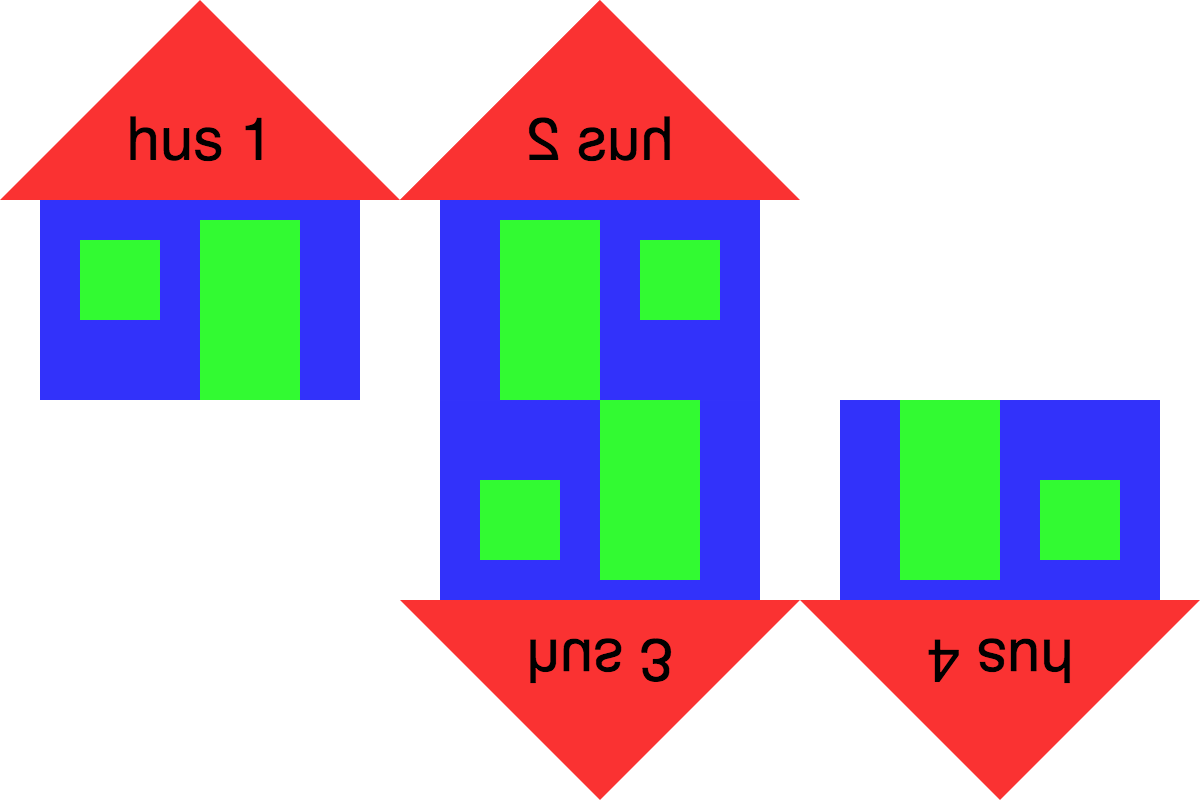
Spegling i \(y\)-axeln kan användas för att rita figurer som är vända i riktning höger eller vänster. Vi kan till exempel göra om den vandrande streckgubben från Loopar och listor: Exempel 11 så att streckgubben går fram och tillbaka och är vänd åt antingen höger eller vänster.
Ladda upp några bilder till OpenProcessing som ska animeras.
Använd följande kod:
var bild = [], index, x, y, riktn, deltax;
function setup() {
createCanvas(windowWidth, windowHeight);
bild[0] = loadImage('stickyFigure1.png');
bild[1] = loadImage('stickyFigure2.png');
bild[2] = loadImage('stickyFigure3.png');
imageMode(CENTER);
index = 0;
x = 0;
y = 350;
riktn = 1;
deltax = 3;
}
function draw() {
background(255);
translate(x, y);
scale(riktn, 1);
image(bild[index], 0, 0, 75, 125);
if (frameCount % 7 == 0) {
index = (index + 1) % bild.length;
}
if ( x > width || x < 0 ) {
deltax *= -1
riktn *= -1;
}
x += deltax;
}Lägg märke till att bilden ritas i origo eftersom koordinatsystemet translaterats.
När man håller på med grafisk programmering är det bra att kunna trigonometri. Även om man inte kan någon trigonometri alls, kan det vara bra att känna till funktionen atan2() vilken finns i många grafiska programmeringsspråk och grafiska matematikprogram som GeoGebra. Funktionen atan2() används för att beräkna vinkeln mellan två punkter i ett koordinatsystem.
Givet en punkt med koordinaterna \( (x_2, y_2) \) och en punkt med koordinaterna \( (x_1, y_1) \), beräknas vinkeln \(v\) som i bilden nedan med funktionen atan2(y2-y1, x2-x1).
Genom att först beräkna en vinkel med hjälp av atan2() och sedan rotera ett objekt denna vinkel, kan vi låta ett objekt peka i riktning mot exempelvis muspekaren.
Med denna kod pekar pilen hela tiden mot muspekaren.
function setup() {
createCanvas(windowWidth, windowHeight);
}
function draw() {
var vinkel;
background(100);
vinkel = atan2(mouseY-height/2, mouseX-width/2);
translate(width/2, height/2);
rotate(vinkel);
pil();
}
function pil() {
fill(255, 0, 0);
noStroke();
rect(0, -10, 20, 20);
triangle(20, -15, 40, 0, 20, 15);
}Man göra pilen kortare eller längre beroende på avståndet till muspekaren. Prova att lägga in raden
scale(dist(mouseX, mouseY, width/2, height/2)/100,1);innan pilen ritas upp i funktionen pil().
Sköldpaddsprogrammering gör det enkelt att använda rekursion för att exempelvis rita ett träd. Genom att translatera och rotera, kan man ganska enkelt rita träd med rekursion i Processing. Vi ska börja med att göra ett träd som bara förgrenar sig i en riktning, sedan göra ett träd som förgrenar sig i två riktningar.
För att rita ett träd med en förgrening åt höger, använder vi följande grundalgoritm:
Rita ett träd
Rita en sträcka rakt uppåt.
Translatera till sträckans övre ändpunkt.
Rotera lite åt höger.
Rita ett träd med en något kortare sträcka.
Nu kan vi inte hålla på att rita ett nytt träd i all oändlighet. Vi kallar antalet sträckor som ska ritas för algoritmens djup och använder parametern djup på följande sätt:
function setup() {
createCanvas(windowWidth, windowHeight);
background(255);
angleMode(DEGREES);
translate(width/2, 0.8*height); // börja rita vid någon position
träd(13, 100);
}
function träd(djup, längd) {
if (djup > 0) { // avsluta rekursionen då djup är noll
strokeWeight(längd/10); // sträckans bredd beror på djupet
line(0, 0, 0, -längd); // rita en sträcka rakt uppåt
translate(0, -längd);
rotate(45);
träd(djup - 1, 0.8*längd);
}
}Ett träd med en förgrening ser ut så här:
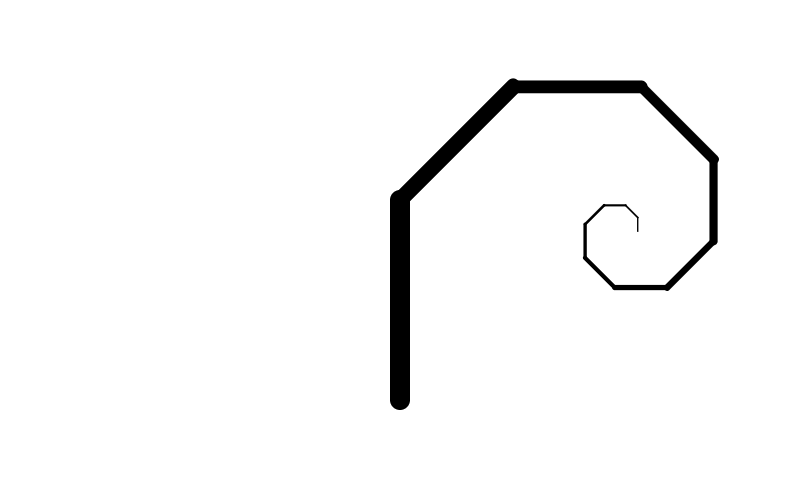
Om vi nu efter att vi vänt oss lite till höger vill vända oss lite åt vänster för att rita en andra förgrening, kan vi börja med att lägga till följande två rader i funktionen träd:
function träd(djup, längd) {
if (djup > 0) {
strokeWeight(längd/10);
line(0, 0, 0, -längd);
translate(0, -längd);
rotate(45);
träd(djup - 1, 0.8*längd);
rotate(-80); //en andra förgrening åt vänster
träd(djup - 1, 0.8*längd);
}
}Detta tillvägagångssätt fungerar dock inte. En del av den bild som ritas upp ser ut så här:

Det som händer när koden körs är att först görs det 12 förgreningar åt höger, sedan görs den första förgreningen åt vänster. När den första förgreningen ät vänster ska ritas upp har vi translaterat och roterat 12 gånger och koordinatsystemet befinner sig vid ändpunkten av den sista sträckan. Koordinatsystem ska dock befinna sig vid samma position när båda förgreningarna börjar ritas upp. När den första förgreningen åt vänster ska ritas upp ska vi bara ha translaterat och roterat 11 gånger.
När den första förgreningen åt höger görs, anropas funktionen träd() vilken translaterar och roterar koordinatsystemet, sedan görs den första förgreningen åt vänster. Vi vill att när den första förgreningen ät vänster görs ska koordinatsystemet befinna sig i samma tillstånd som då förgreningen åt höger gjordes. För att kunna åstadkomma detta behöver vi kunna spara undan koordinatsystemets tillstånd innan vi translaterar och roterar. Efter att båda förgreningarna gjorts vill vi kunna återgå till det senast sparade tillståndet. Det finns två funktioner som gör just detta.
push() sparar koordinatsystemets tillstånd.pop() återgår till det senast sparade tillståndet.Vi lägger in dessa funktioner i koden:
function träd(djup, längd) {
if (djup > 0) {
strokeWeight(längd/10);
line(0, 0, 0, -längd);
push(); // spara koordinatsystemets tillstånd
translate(0, -längd);
rotate(45);
träd(djup - 1, 0.8*längd);
rotate(-80);
träd(djup - 1, 0.8*längd);
pop(); // återgå till senast sparade tillstånd
}Nu ritas trädet upp som det ska se ut.

Rita bild med kod
Utgå ifrån koden i Exempel 1. Byt koden som ritar bilden mot valfri kod, rita exempelvis ett hus, en smiley eller annat. Tänk på att \(y\)-axeln ökar i riktning neråt.
Studsande polkagriseffekt
Utgå ifrån koden i Exempel 3. Skriv dit kod som gör att bilden studsar i kanten.
Dataspel med rotation
Gör något dataspel med rotation, exempelvis Geometry Dash eller Flappy bird (i Flappy Bird kan fågeln rotera fast inte hela varvet runt).
Dataspel med spegling
Gör något dataspel med spegling. Det går exempelvis att göra en variant av Frogger som beskrivs på sidan Kom igång med Scracth: Uppgift 6.
Sikta och skjut
Utgå ifrån koden i Exempel 6. Gör något spel som handlar om att sikta och skjuta.
Varianter av träd
Implementera koden för att rita ett träd som beskrivs under rubriken Rekursion. Testa att göra varianter exempelvis genom att:
Koch-kurva
Utgå ifrån koden:
function setup() {
createCanvas(windowWidth, windowHeight);
background(255);
angleMode(DEGREES);
translate(0.1*width, 0.6*height);
koch(1, 0.8*width);
}
function koch(djup, längd) {
if (djup == 0) {
line(0, 0, längd, 0);
} else {
koch(djup - 1, längd/3);
// kod för att rita ytterligare tre Koch-kurvor
}
}Fyll i den kod som saknas. Koden ska använda translationer och rotationer för att åstadkomma den röda, gröna och blå sträckan om koch(1, 0.8*width); anropas i setup-funktionen (sträckorna behöver dock inte ha olika färg). Se till att koordinatsystemets tillstånd sparas innan du utför transfornationerna. Återgå till det senast sparade tillståndet i slutet.
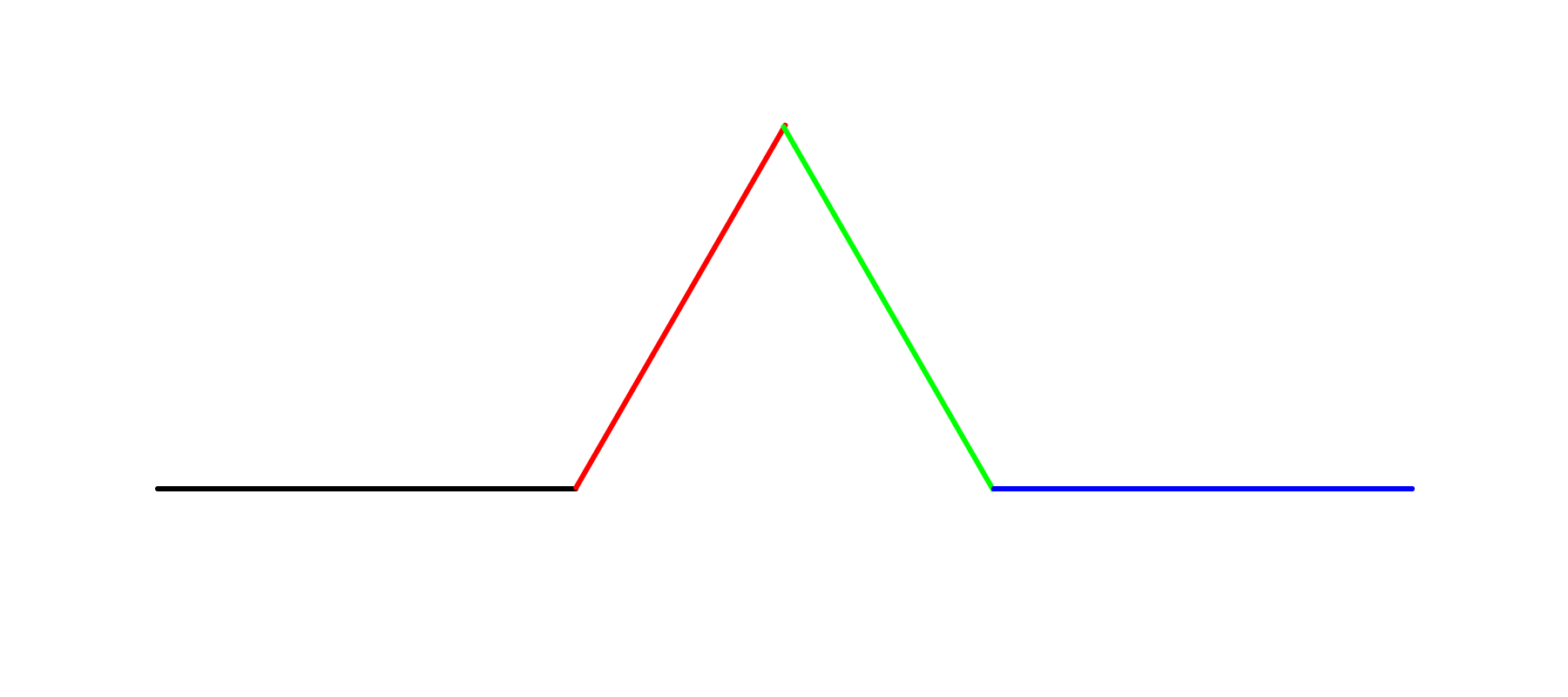
När du är klar ska anropet koch(7, 0.8*width); i setup-funktionen rita upp följande kurva:
