

Eftersom blockprogrammering är ett visuellt hantverk, är det bästa sättet att komma igång med blockprogrammering att se hur detta hantverk utförs och sedan testa själv.
Se videon Kom igång med Scratch
för att lära dig hur man:
Se videon Bakgrund, sprajtar och enkel styrning.
för att lära dig hur man:
Se videon Enkelt spel med poängräkning
för att lära dig hur man:
Se videon Kollisioner
för att lära dig hur man:
Se videon Tangentstyrning med hinder
för att lära dig hur man:
Se videon Styrning med muspekare och hinder
för att lära dig hur man styr en sprajt på olika sätt med muspekare och undviker hinder.
Se videon Finjustering av poängräkning
för att lära dig hur man delar ut exakt en poäng, på två olika sätt.
Se videon Pennverktyg
för att lära dig hur man:
Se videon Egna block och generaliseringar
för att lära dig hur man:
Se videon Text och slumptal
för att lära dig hur man:
Se videon Listor
för att lära dig hur man skapar och använder listor.
Se videon Slumptal och fallande rörelse
för att lära dig hur man gör en upprepad fallande rörelse från en slumpmässig position med och utan acceleration.
Se videon Enkla och avancerade hopp
för att lära dig hur man modellerar hopp med och utan acceleration.
Se videon Från fart till hastighet
för att lära dig hur man modellerar rörelse i x- och y-led.
Se videon Kloner
för att lära dig hur man använder kloner.
Se videon Rekursion
för att lära dig hur man använder rekursion för att göra självupprepande mönster.
Självupprepande mönster, så kallade fraktaler, skapade med hjälp av slumptal används bl.a. av filmindustrin för att datorgenerera berg, träd, moln, m.m. Se exempelvis Wikipedia: Fractal landscape för mer information.
Att lära sig programmera handlar dels om att lära sig hur något programmeringsspråk fungerar och dels om att lära sig vissa grundläggande principer som återkommer inom många programmeringsspråk.
Här följer några grundläggande programmeringsprinciper i Scratch.
En sekvens är ett antal ihoppusslade kodblock som genomförs i ordningen uppifrån och ner när programmet körs.
En sekvens kan ligga under en händelse eller inuti ett u-format block.

En upprepning kallas också för en iteration. Att upprepa kallas också för att itererera.
Det finns tre olika upprepningar i Scratch.

Att upprepa något många gånger är något som datorer är bra på. Alla programmeringsspråk innehåller strukturer för att upprepa.
Att utföra olika instruktioner beroende på vilken situation som råder, görs i Scratch med om-block eller om-annars-block. Vilken situation som råder avgörs med ett så kallat villkor. Ett villkor är ett logiskt uttryck. Ett logiskt uttryck kan bara anta två värden, det kan vara sant eller falskt. Alla logiska uttryck i Scratch beskrivs med block som är sexhörningar.
Ett alternativ inom programmering utförs alltid med hjälp av villkor, ibland kallas därför ett alternativ för en villkorssats. Ibland används också ordet selektion.
Om man i Scratch vill använda flera olika villkor som alla beskriver samma situation, kan man lägga om-block inuti om-block.

Alla programmeringsspråk innehåller strukturer för alternativ.
En så kallad händelse utlöses exempelvis av att användaren klickar med musen eller använder en tangent på tangentbordet. Programmeringsspråk som hanterar händelser kallas för händelsestyrda.
För de flesta vanliga programmeringsspråk är händelsehantering så pass komplicerat att nybörjare i programmering inte lär sig hantera händelser. I Scratch är händelsestyrning ett så centralt begrepp att även de yngsta barnen som lär sig programmera i Scratch, lär sig hantera händelser.
Det är händelsestyrning som gör ett program interaktivt, dvs användaren kan interagera med programmet för att bestämma vad programmet ska göra.
Under kategorin Händelser i Scratch, finns bl.a. blocket när-flagga-klickas-på, vilket inte gör något annat än att starta programmet. Eftersom även icke-händelsestyrda program kan startas, brukar inte detta i andra sammanhang räknas som en händelse.
I Scratch kan man göra egna variabler under kategorin data. Att göra en variabel kallas för att deklarera en variabel ‐ man deklarerar för programmet vilka variabler man ska använda.
En variabel har ett namn och ett värde. Värdet kan variera. En variabel med namnet poäng kan ha värdet 7.

En variabel som deklareras Enbart för denna sprajt, kan bara användas av den sprajt som är markerad när variabeln görs. En sådan variabel sägs vara lokalt deklarerad. Om variabeln poäng deklarerars enbart för katt-sprajten, kan ingen annan sprajt ändra eller sätta poängen.
En variabel som deklareras För alla sprajtar sägs vara globalt deklarerad.
Om man gör ett långt program som innehåller många variabler, är det en god princip att deklarera variabler så lokalt som möjligt. En stor del av en programmerares tid går åt till att hitta fel i program. Om en variabels värde kan ändras överallt i ett program, kan det vara svårt att hitta fel.
När du gör ett eget block i Scratch, definierar du vilken kod som ska utföras när blocket används. Denna kod utförs när du sedan använder blocket.

Ett egendefinierat block kan använda värden som skickas in i blocket när det används. Sådana värden kallas för parametrar. I bilden ovan är namn, tal1 och tal2 parametrar. De värden som skickas in till blocken är Hugo, 78 och 124; dessa värden är argument.
I Scratch kan du lägga in så kallade etiketter när du gör ett block. Etiketter används för att med text förklara vad blocket görs.

Inom andra programmeringsspråk används inte block men principen att man definierar ett stycke kod som kan användas på flera ställen i programmet, och som kan ta emot värden, är en grundläggande princip för de flesta programmeringsspråk. Det namn som används för denna princip varierar beroende på programmeringsspråk, det kan kallas för funktion, metod eller subrutin. Vi kommer att använda ordet funktion.
Att använda en funktion kallas för att anropa funktionen. Detta motsvaras i Scratch av att använda det egendefinierade blocket.
De värden som skickas in till en funktion kan också kallas för argument. Ska man vara noga används ordet parameter för de namn som används vid definitionen ( namn, tal1, tal2) och ordet argument för de värden som skickas in till funktionen (Hugo, 78, 124). Ofta gör man dock ingen skillnad mellan orden argument och parameter utan använder orden omväxlande för att beteckna samma sak, värden som skickas in till och används av en funktion.
Scratch skiljer mellan tre olika sorters datatyper
Ett block som innehåller ett talvärde, representerar detta med en vit ellips. Ett block som innehåller ett textvärde, representerar detta med en vit rektangel.

Ett logiskt värde kan bara anta två värden, sant eller falskt. Inom programmering kallas ett logiskt värde för ett boolskt värde eftersom så kallad boolesk logik används. Inom boolesk logik används talet 1 för sant och talet 0 för falskt. Ett booleskt värde representeras i Scratch av block som är sexhörningar.

När du deklarerar en variabel i Scratch, behöver du inte ange vilken sorts datatyp variabeln ska vara. Det går bara att använda variabler som representerar text eller tal. Det går inte att göra variabler som är sexhörningar.
När du gör ett eget block i Scratch, måste du ange vilken sorts datatyper eventuella parametrar ska vara.

Hur gör man då om man vill göra en variabel som antingen är sann eller falsk. Jo, man gör en variabel som är ett tal och låter 1 representera sann och 0 representera falsk. För att kolla om värdet är "sant", kollar man om värdet är 1. För att byta värde mellan sann och falsk, använder man konstruktionen nedan:
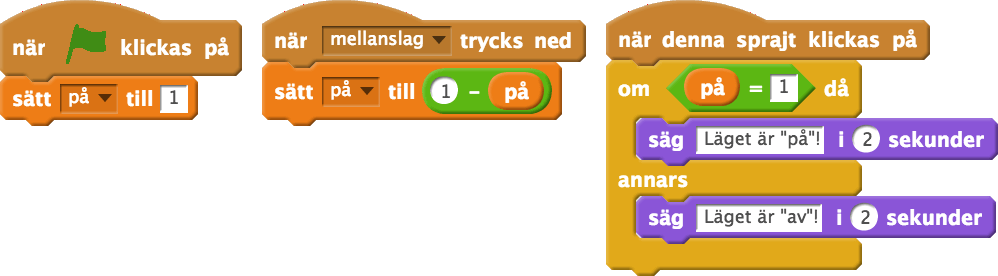
På detta vis använder man aritmetik för att hantera logik, vilket är precis hur boolesk logik fungerar.
Alla programmeringsspråk använder sig av datatyper. Det används oftast olika datatyper för tal, en typ för heltal (134, -86) och en typ för decimaltal (3.14, -0.9). Vissa programmeringsspråk har en datatyp för tecken ('a', 'ö', '€', '<'). De flesta programmeringsspråk har någon datatyp för text. Text skrivs oftast mellan citationstecken, det är alltså skillnad på texten "3.14" och talet 3.14. De flesta programmeringsspråk brukar använda de två värdena true och false för booleska variabler.
Det som i Scratch kallas för klon, kallas inom andra programmeringsspråk för objekt. Programmeringsspråk som låter programmerare definiera och använda objekt, kallas för objektorienterade programmeringsspråk.
Ett objekt inom programmering är en struktur som kan innehålla ett antal värden och ett antal metoder som objektet kan utföra. I regel används objekt om man vill göra många uppsättningar av samma sak. Om man exempelvis vill att ett antal bollar ska studsa runt på en skärm, definierar man någonstans en boll. En boll kan ha värden som radie, färg och startposition. Den kan ha en metod studsa omkring. När man väl definierat sitt objekt boll, kan man skapa en boll med en given radie, färg och startposition. Sedan kan man använda metoden studsa omkring. Man kan därefter på ett enkelt sätt skapa många studsande bollar.
Inom de flesta programmeringsspråk kan man som programmerare göra indexerade listor. En indexered lista lagrar värden på numrerade positioner.
I Scratch kan man skapa en lista och sedan lägga in värden i listan innan programmet körs (genom att klicka på plus-tecknet i listans nedre vänstra hörn). Ett annat vanligt användningsområde är att fylla listan med värden när programmet körs. Ett sådant exempel visas i koden nedan. Programmet är ett ritprogram som lagrar positioner i två listor x och y. När sedan mellanslag klickas, ritas vägen mellan positionerna ut med en annan färg.
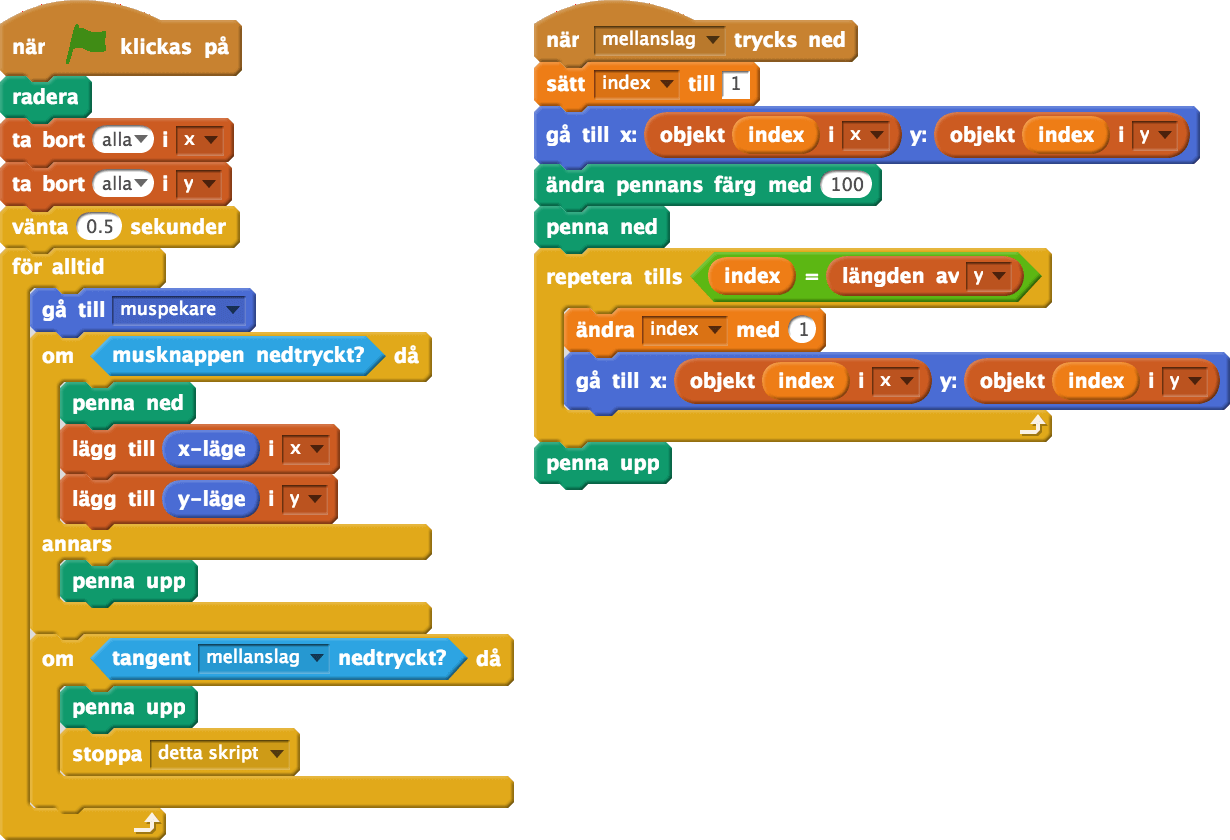
Testa gärna att göra två listor x och y och kopiera koden i bilden ovan. Vilken bild ritas upp om man under mellanslag istället använder följande kod:

När du börjar undervisa Scratch för nybörjare är det nästan oundvikligt att undervisningen går till på så vis att du visar hur man gör och eleverna gör exakt samma sak som du nyss gjorde, exempelvis "så här pusslar man ihop block".
När man tagit sig förbi den mest grundläggande hanteringen av kategorier, block, sprajtar, bakgrunder, m.m.; handlar det om att hitta en balans mellan tydliga instruktioner (som eleverna härmar) och uppgifter som låter eleverna skapa fritt.
Några exempel på undervisningsmetoder som både innehåller tydliga instruktioner och fritt skapande är:
Programmeringsämnet erbjuder många möjligheter att testa sig fram och det är bra om man som lärare uppmanar elever att göra just detta: testa att köra programmet, se efter vad som händer om du ändrar det värdet, vad händer om du byter det blocket mot det där.
Många program behöver justeras på slutet för att fungera på ett bra sätt. Detta kan beskrivas som en tinkering-process där programmeraren omväxlande ändrar i koden och testkör programmet. Att ägna sig åt sådan tinkering är en del av att lära sig programmera och denna process ingår automatiskt i de flesta programmeringsövningar. Som lärare kan man göra övningar just för att öva upp tinkering-förmågan, exempelvis övningar där eleverna ska utgå från kod som måste justeras för att fungera på ett bra sätt. Ett sätt att göra tinkering-övningar är att skapa kod i Scratch som eleverna sedan remixar och gör om.
Detta att göra små justeringar och att testa olika metoder för att få någonting att fungera är en allmän problemlösningsförmåga som kan användas i många andra sammanhang, även inom matematisk problemlösning.
Att lära sig programmera innefattar att man lär sig hitta programmeringsfel. Felaktig kod sägs innehålla buggar efter det engelska ordet bug, se exempelvis Wikipedia: Software bug. Att hitta och rätta till felaktig kod kallas för att avlusa programmet på svenska (debug på engelska). Som lärare kan man göra så kallade avlusningsövningar, dvs program som avsiktligt innehåller fel. En avlusningsövning innehålla en skriftlig beskrivning av hur programmet borde fungera och kod som inte fungerar som det är tänkt. Elevens uppgift är att hitta felet och rätta till koden. I Scratch kan avlusningsövningar göras som remix-övningar men det går också att dela ut felaktig kod i pappersformat och be elever, enskilt eller i grupp, beskriva varför koden inte fungerar. Om övningen görs som en remix-övning kan man skriva i rutan Instruktioner hur programmet borde fungera.

Förutom att eleverna med avlusningsövningar övar på felsökning, kan sådana övningar också användas till att få eleverna att reflektera kring hur kod fungerar. Framför allt yngre elever kan kopiera kod som andra har gjort och sedan inte ägna en tanke åt varför koden fungerar. Avlusningsövningar kan i sådana fall fungera som ett sätt att tvinga fram reflektion.
Ett enkelt sätt att samla in elevarbeten är att använda en så kallas Scratch-studio. För att göra en studio går du till din profil i det övre högra hörnet och väljer Mina grejer. Uppe till höger finns det en knapp för att göra en ny studio. I menyn till vänster kan du gå in och hantera de studior du gjort.

När du skapar studion ger du den ett namn och markerar att alla ska kunna använda studion (inte bara du). Eleverna kan därefter gå in till din studio och klicka på Lägg till projekt

Det går också att göra ett så kallat lärarkonto som ger utökad funktionalitet för just verksamma lärare, se exempelvis Scratch Lärarkonto FAQ eller Scratch för pedagoger för mer information.
I nuläget ingår inte programmering i de nationella proven för matematik och det finns inga officiella beskrivningar av kunskapskrav. Hur du bedömer elevarbeten avgör du alltså själv. Tänk på att det kan vara vanskligt att bedöma elevprogram som innehåller en mängd olika moment som inte har med matematik att göra. Ett välfungerande program kan ha en bra design och fungera på ett bra sätt även om programmeringen i sig inte är avancerad eller innehåller något som är matematiskt intressant. Det är också svårt att bedöma program som är gjorde som remix och det är allmänt svårt att avgöra huruvida en elev skapat koden själv eller kopierat från någon annan.
Detta att man som programmerare använder kod som andra gjort är mycket vanligt inom programmering. Genom att programmerare vidareutvecklar varandras kod bidrar de till att koden förbättras. Den kod som används för att göra Scratch 3.0 finns tillgänglig på det så kallade Github. Koden kan laddas ner på sidan Github: Scratch och är så kallad Öppen källkod. Att elever använder andras kod ska alltså inte ses som någon sorts "fusk", utan som ett sätt för dem att lära sig programmering ‐ trots att detta gör bedömning något svårare. Det är också lärorikt att låta elever programmera i grupp. Inom programmering är det vanligt att så kallad parprogrammering används, se exempelvis Pair programming (engelska) för en beskrivning.
En metod för bedömning är att använda programmeringsuppgifter som obligatoriska inlämningsuppgifter som inte bedöms på annat sätt än godkänd eller icke godkänd och att använda andra sätt för att mäta kvalité. Det går exempelvis att göra skriftliga prov i programmering. Du kan se exempel använda i ett forskningsprojekt på mellanstadienivå. Dessa exempel användes inte för betygsättning utan för att få eleverna att reflektera och diskutera: Sekvenser, upprepningar & händelser, Felaktig kod, Rörelse i koordinatplan.
Ett matematiskt problem på grundskolenivå är ofta strukturerat som en mer eller mindre klurig fråga som har ett svar som antingen är rätt eller fel. Det finns få sådana matematiska problem på grundskolenivå som med fördel löses med hjälp av programmering. På universitetsnivå, eller i gymnasiets högre kurser, finns det problem som inte kan lösas på andra sätt än med numeriska metoder. Det finns också gott om problem som visserligen kan lösas för hand men som är så pass tidsödande att det är enklare att skriva ett program som löser alla problem av samma sort. På grundskolenivå är det kanske inte denna sorts matematisk problemlösning som bör kopplas ihop med programmeringsundervisning.
Programmering används ofta till den sortens matematisk problemlösning som handlar om modellering och simulering. En matematisk modell kan användas för att beskriva någon verklig situation och programmering används för att simulera situationen. Det kan exempelvis handla om hur en sjukdom sprids, hur köer på banken fluktuerar över en dag, hur flyttfåglar rör sig, hur en rymdraket styrs mellan himlakroppar, m.m. När en grundskoleelev gör ett dataspel ingår det ofta att karaktärer rör sig, denna rörelse följer någon matematisk modell som datorprogrammet simulerar.
Förutom kopplingen mellan matematisk modellering och programmering, finns det ofta en koppling mellan matematik och programmering på så vis att elever övas i att använda matematiska begrepp när de programmerar. I dessa fall är det inte matematiken i sig som är målet, matematiken är istället ett verktyg för att datorprogrammet ska fungera. Programmering är en tillämpning som innehåller mer matematik än de flesta andra tillämpningar relevanta för grundskoleelever.
Vi nämner här några matematiska begrepp som är vanliga inom Scratch-programmering.
Elever lär sig ofta förstå begreppet vinkel i lägre årskurser än på högstadiet. Definitionen av en vinkel är abstrakt och elever lär sig ofta förstå vinkelbegreppet genom att mäta vinklar med en gradskiva.
Istället för att använda en bild av en vinkel, kan man beskriva en vinkel med hjälp av rotationer. En vinkel är ett mått på hur mycket någonting roterar. Inom sköldpaddsprogrammering är en vinkel ett mått på hur mycket en sprajt vänder sig. Med detta synsätt lärs vinkelbegreppet ut som en process, processen att vända en sprajt. För vissa elever kan det vara enklare, och kännas mer meningsfullt, att lära sig begrepp med hjälp av processer istället för abstrakta och svårbeskrivna ting. Det är dessutom så att elever i allmänhet får en större förståelse för ett begrepp om de kommer i kontakt med olika representationsformer för begreppet.
Även om processen att gå och vända är en enkel process kan man rita komplicerade matematiska mönster om man exempelvis ökar vinkeln i varje steg. Testa exempelvis koden:
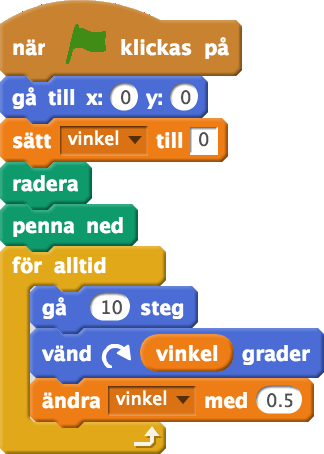
Resultatet är en så kallad Cornu spiral. Det går att göra många olika varianter av spiralen genom att variera hur mycket vinkeln ökar.

Det är vanligt att yngre elever uppfattar likhetstecknet inte som en likhet utan som verbet "blir", exempelvis tolkas \(4+5=9\) som "fyra plus fem blir nio". Detta att en likhet ska uppfattas som någonting som antingen är sant eller falskt, är en förståelse som krävs för ekvationslösning och inom andra delar av matematiken. Att lösa en ekvation i variabeln \(x\) innebär att man listar ut vilka värden på \(x\) som gör ekvationen sann. En ekvation kan sakna lösningar, exempelvis finns det inga reella tal \(x\) som gör ekvationen \(x^2 = -1 \) sann. En kurva kan definieras av en ekvation. Ekvationen \(y = 5x+2\) definierar en kurva som består av alla de punkter \((x, y) \) som uppfyller ekvationen, dvs de punkter som gör ekvationen sann.
Inom programmering används likhet just som en logisk likhet. Följande kod

används för att kontrollera om användaren svarat rätt i ett multiplikationsprogram. En del elever har svårt för att förstå koden vilken förutom begreppet likhet också använder sig av tre variabler. Som lärare kan det vara värt att tänka på att likheten här används just som någonting som är antingen sant eller falskt, det vill säga på ett sätt som inte alla elever från början förstår.
Olikheter används ofta i gymnasiets matematik för att beskriva situationer som handlar om "minst" eller "högst". Ett enkelt problem kan vara:
Lisa sommarjobbar och tjänar \(130\) kr i timmen. Hon vill köpa en mobiltelefon för \(3\, 510\) kr. Hur många timmar måste hon minst jobba för att ha råd med mobiltelefonen? Beskriv problemet som en olikhet och lös olikheten.
Tanken är att lösningen ska se ut så här: Låt \(x\) vara antalet timmar.
\[ \begin{align} 130x &\ge 3\,510 \\ x &\ge \frac{3\,510}{130} \\ x &\ge 27 \end{align} \]Problemet kan dock lika gärna lösas som en ekvation och på slutet kan man resonera sig fram till att hon inte ska jobba exakt \(27\) timmar utan minst \(27\) timmar, dvs olikheterna behövs inte utan det räcker att använda ekvationslösning och vanligt bondförnuft. Olikheter används mycket och behövs inom högre matematik men det är svårt att i skolan motivera varför eleverna ska lära sig hantera olikheter.
Inom programmering är olikheter mycket vanliga och kan oftast inte ersättas av likheter. Följande kod låter en sprajt falla till marken. Marken börjar där \(y\)-koordinaten är -100.

Det går i det här fallet inte att använda likhet eftersom \(y\)-koordinatens exakta värde när sprajten når marken inte är känd. Det är dessutom så att om decimaltal används inom programmering ska likheter alltid undvikas eftersom decimaltal inte representeras exakt av en dator.
I skolans matematikundervisning används variabler inom algebran. En typisk skoluppgift kan vara att skriva ett uttryck i variabeln \(x\) för en geometrisk figurs omkrets.
Den geometriska figuren kan användas till ekvationslösning: Om omkretsen är 49 cm, vilket värde har då \(x\)?
När variabler används inom Scratch-programmering, får eleverna inte alltid lära sig lika många metoder som i matematikundervisningen. I geometriproblemet ovan ingår metoder för att förenkla uttryck samt att ställa upp och lösa en ekvation. Det programmeringen kan bidra med är att motivera varför variabler behövs i vissa sammanhang. Principen att man använder ett namn som poäng eller bokstaven \(x\) för att beteckna något som kan anta olika värden, den principen gäller både inom programmering och i skolans algebraundervisning.
På liknande sätt kan programmering användas för att motivera varför det i vissa fall är förnuftigt att generalisera. När man programmerar ett matematiskt verktyg som en regelbunden \(n\)-hörning är det lätt att motivera varför man bara gör ett enda verktyg. Det är behändigt att betrakta det allmänna fallet snarare än att hantera varje specialfall (trehörning, fyrhörning, femhörning, ...) för sig. För att kunna behandla det allmänna fallet måste man kunna skriva ett uttryck i \(n\) för vilka vinklar som ska användas för \(n\)-hörningen. Vi har alltså här samma situation som i geometriproblemet ovan, vi måste kunna beskriva ett uttryck med hjälp av en variabel.
Sköldpaddsprogrammering använder sig av det matematiska begreppet vinkel. En sprajt rör sig framåt i en riktning där riktningen mäts mot den positiva \(y\)-axeln. Vinkeln ökar om man går i medurs riktning från den positiva \(y\)-axeln.
För enklare rörelse fungerar sköldpaddsprogrammering väl och man kan exempelvis använda blocket studsa-vid-kanten som byter riktning, men säg att man vill studsa vid någonting annat än kanten exempelvis en paddel som används i spelet Pong. Då finns det inget färdiggjort block utan man måste själv lista ut hur riktningen ska förändras.
Det går att visa att om riktningen från början är \(x\), så är den efter studsen \(180^\circ -x\). Det går alltså att använda koden:

Att visa detta samband mellan riktningarna före och efter studs, är relativt svårt för en högstadieelev. Det går heller inte att överföra metoden till andra programmeringsspråk, språk som inte är gjorda specifikt för barn. Om man vill använda sig av riktning och vinklar i sådana språk, måste man kunna trigonometri, vilket högstadieelever inte kan. Dessutom är det så att vid mer avancerad modellering av rörelse används inte vinklar utan vektorer.
Istället för att använda sköldpaddsprogrammering och vinklar, kan man behandla all rörelse som förflyttningar längs \(x\)-axeln och \(y\)-axeln. Om rörelsen är en förflyttning 7 enheter längs \(x\)-axeln och 5 enheter längs \(y\)-axeln, blir den sammanlagda förflyttningen den som motsvaras av en vektoraddition. En vektor har en storlek och en riktning och brukar ritas ut som en pil. I bilden nedan visas addition av två vektorer \(u\) och \(v\).
En studs vid höger kant gör att vektorn \(u\) ska byta till motsatt riktning, det är lätt att förstå att detta ger att infallsvinkeln är lika med reflektionsvinkeln.
Om paddeln befinner sig längst ner i fönstret kan följande kod användas för Pong:

Här används inte "rör vid kanten", istället används olikheter och koordinater för att ta reda på när sprajten befinner sig i närheten av en kant. Om sprajten är vid den vänstra eller högra kanten ska variabeln x-hastighet byta tecken. Om sprajten är vid den övre eller nedre kanten, eller rör vid paddeln, ska y-hastighet byta tecken. Denna metod kan direkt överföras till andra programmeringsspråk, språk som inte är gjorda specifikt för barn. Den enda svårighet som kvarstår är i sådana fall att avgöra när sprajten rör vid paddeln.
För framför allt yngre elever kan det vara svårt att hantera alla de olika kodblock som i Scratch används för rörelse.
Vissa kodblock ger en absolut rörelse på så vis att det spelar inte spelar någon roll vilka värden rörelsevariablerna hade från början. Det spelar ingen roll hur en sprajt var vänd från början, använder man blocket peka-i-riktning-höger, kommer den att peka åt höger. Var den redan vänd åt höger, händer det ingenting när man använder blocket.

Det kan vara speciellt svårt att förstå blocket glid.

Om sprajten redan befinner sig på positionen \(x = 100, y = 100\), händer det ingenting när man använder blocket glid.
Andra rörelseblock förändrar de värden rörelsevariablerna har.

Rörelsen är med dessa block relativ eftersom någon eller några rörelsevariabler förändras.
På samma sätt kan det vara svårt att förstå skillnaden mellan att sätta en variabels värde och att ändra värdet. Att ändra en variabels värde innebär att man adderar till det som står i den vita rutan till det värde variabeln hade från början.

Om variabeln från början har värdet 10, kommer den att få värdet 5 om sätt-blocket används och värdet 15 om ändra-blocket används. Som lärare kan man behöva poängtera denna skillnad mellan att sätta och att ändra.
En av de största kopplingarna mellan Scratch-programmering och högstadiets kursplan i matematik är kopplingar till det som i kursplanen kallas Samband och förändring.
Inom matematikundervisningen går man igenom sträcka, hastighet och tid genom att använda formeln
\[v = \frac{s}{t}\]på olika sätt. I denna undervisning brukar det ingå att byta enheter och att eventuellt rita så kallade st-diagram eller vt-diagram för att beskrivs hur sträckan respektive hastigheten förändras över tiden.
Inom Scratch-programmering används samma samband mellan sträcka, hastighet och tid men sambandet används på ett helt annat sätt. Tidsenheten är alltid densamma. För en snabb dator tar varje tickning ungefär en 60-dels sekund. Längdenheten är alltid hur lång sidan i en pixel är. En pixel är den minsta ruta en datorskärm är uppbyggd av. Eftersom olika datorskärmar har olika stora pixlar, finns det inget enkelt sätt att byta enhet till exempelvis cm.
Inom matematikundervisning används st-diagram eller vt-diagram för att visualisera en rörelse. Med hjälp av grafen kan man dra slutsatser om rörelsen. Om grafen i ett st-diagram har en stor lutning, innebär detta att objektet rör sig snabbt. I Scratch-programmering visualiseras rörelsen direkt genom att objekt faktiskt rör sig.
I och med att rörelsen visualiseras direkt, finns det anledning att tala om riktningar och att skilja på begreppen fart och hastighet. Om sköldpaddsprogrammering används, och en sprajt hela tiden rör i riktningen "framåt", har sprajten en fart. Om koordinatsystem används, och om en sprajt hela tiden rör sig genom att ändra \(x\)- och \(y\)-koordinat, har sprajten en hastighet i \(x\)-led och en hastighet i \(y\)-led. Den faktiska rörelsen har en hastighet som är en sammansättning av dessa två hastigheter, en sammansättning som motsvarar en vektoraddition.
Man kan accelerera en sprajt oavsett om fart eller hastighet används. Om hastighet används och om man accelererar sprajten neråt, motsvarar detta den acceleration jordens dragningskraft åstadkommer genom gravitation. Att programmera ett hopp innefattar alltså en matematisk modell som simuleras av datorprogrammet.

Variabeln fart anger hur mycket läget förändras per tidsenhet. Om farten per tidsenhet ändras med 1 pixel, är accelerationen 1 pixel/tidsenhet. Detta resonemang leder i gymnasiets matematikkurser till hur man definierar derivatan. Farten fås genom att man deriverar sträckan med avseende på tiden. Accelerationen fås genom att man deriverar farten med avseende på tiden. Accelerationen kan också ses som andra derivatan av sträckan med avseende på tiden.
Att i varje tidsenhet ändra läget med variabeln fart, motsvaras i gymnasiets matematikkurser av att man integrerar. Den kod som används för rörelse med hastigheter använder samma metod som används för att lösa differentialekvationer numeriskt. Numeriska lösningar av differentialekvationer har traditionellt ingått i gymnasiets högre kurser och på universitetsnivå.
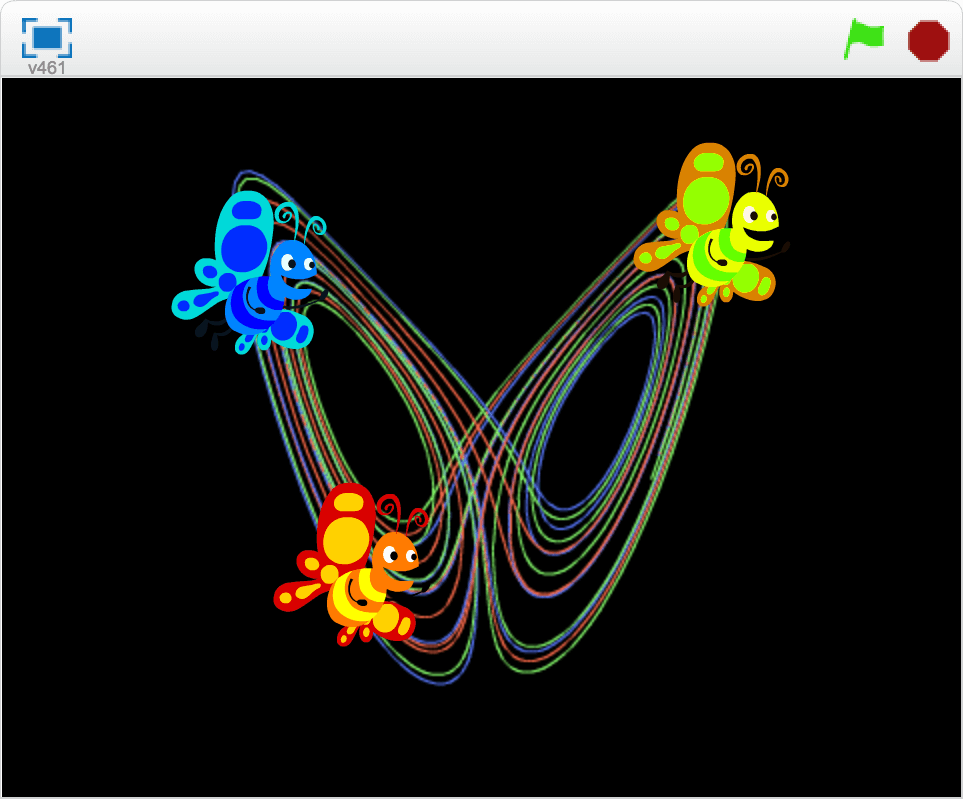
En mycket känd numerisk lösning av en differentialekvation är den så kallade Lorenz-attraktorn vilken meteorologen Edward Lorenz beskrev som ett exempel på ett kaotiskt system. En Lorenz-attraktor i Scratch kan programmeras med en metod som påminner om hur man programmerar ett hopp, hastigheterna i olika riktningar förändras dock på ett mer komplicerat sätt än vid ett enkelt hopp.
Enkelt spel med poängräkning
Gör ett spel där en sprajt hela tiden rör sig och studsar vid kanten. Lägg in en variabel poäng och ge spelaren poäng varje gång sprajten träffas med muspekaren. Se till att något händer när spelaren fått en viss poäng.

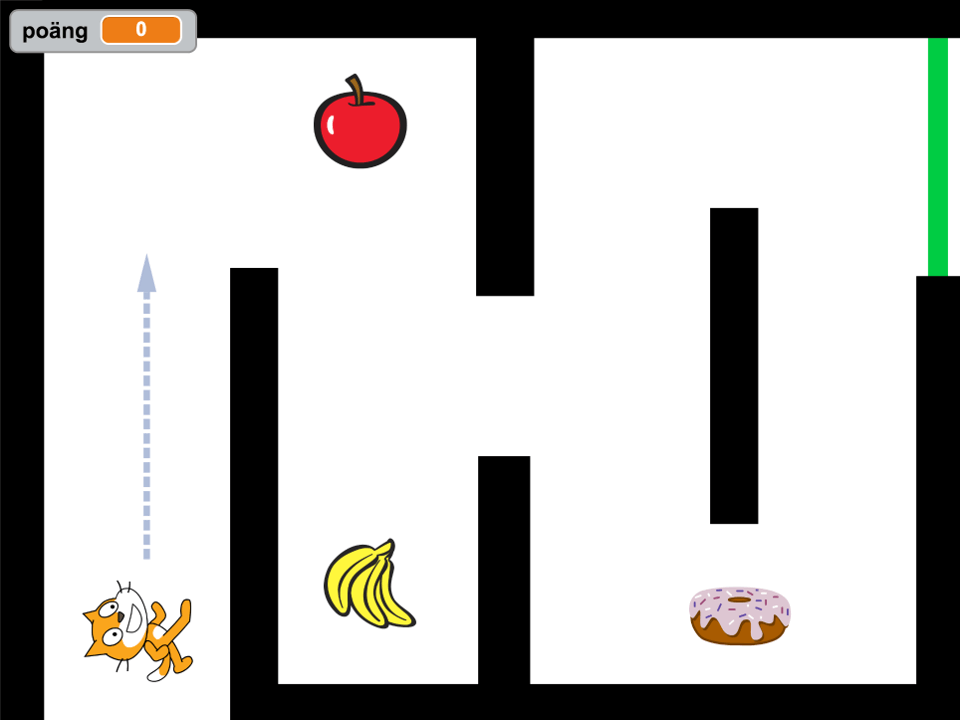
Labyrintspel
Se till att spelaren kan styra en sprajt genom en labyrint. Välj själv hur sprajten ska styras. Se till att sprajten börjar om på startpositionen varenda gång den går in i väggen. Se till att något händer när sprajten når målet.
Du kan antingen rita en egen labyrint som bakgrund eller välja en färdiggjord labyrint. Sök på "labyrint utan kod" i sökrutan i Scratch för att använda en färdiggjort bakgrund. Klicka på remix för att remixa koden.
Multiplikationsmaskin
Låt en sprajt ställa frågan Vad är 5*7?, låt användaren besvara frågan och visa sedan ett meddelande om huruvida användaren svarat rätt. De tal som används ska vara slumptal så att frågan handlar om olika tal varenda gång programmet körs.

Rita mönster
Gör ett eget block som ritar en kvadrat och som har en parameter som används för kvadratens sidlängd. Se till att kvadraten ritas upp utan skärmuppdatering. Använd blocket för att rita spiralliknande mönster genom att låta sprajten rotera i en loop. Se till att kvadratens sida ökar, för att åstadkomma detta behövs en variabel för kvadratens sida.
Detta program har relativt hög abstraktionsnivå. Det finns en parameter för kvadratsidan som används i definitionen av kvadratblocket. För att rita en kvadrat med sidan 100, skickas värdet 100 in till blocket. För att rita kvadrater som är större och större, används en variabel vars värde skickas in som värde till blocket. Svårigheten med detta program är inte geometri (att en kvadrat har 90-graders vinkel) utan hanteringen av variabler.

Gör ett block som istället ritar en n-hörning och gör mönster genom att variera antalet hörn.

Fånga äpplen
Gör ett program där ett äpple (eller annan sprajt) hela tiden faller från en slumpmässig position i den övre delen av fönstret. Fånga äpplen med en skål (eller annan sprajt) som bara kan röra sig x-led längst ner i fönstret. Ge spelaren poäng för varje äpple som fångas.

Frogger
Frogger är ett klassiskt spel i vilket en groda ska ta sig förbi hinder för att komma hem. Hindren kan vara stockar som flyter i en flod, bilar som kör på en väg, alligatorer som simmar i vatten, eller annat.
Grodan startar längst ner i fönstret och hemmet är överst i fönstret. Hindren rör sig fram och tillbaka över fönstret. Spelaren ska styra godan hem och undvika hindren.
Ett enkelt sätt att får sprajtar att glida fram och tillbaka, är att använda blocket glid (under kategorin Rörelse).

Gör en variabel liv. Se till att grodan startar med 10 liv och att den förlorar liv varenda gång den går in i ett hinder. Se till att något händer när grodan förlorat alla liv och att något annat händer när grodan kommit hem.
Geometry Dash
Geometry Dash är ett populärt spel för mobiler och tablets som är utvecklat i Sverige. Spelet går ut på att en kvadrat ska hoppa över olika geometriska figurer.
Börja med att göra två sprajtar: en kvadrat som ska hoppa och en sprajt med flera klädslar (exempelvis trianglar) som ska komma in från höger.
Kvadraten ska hoppa när användaren klickar på mellanslag (eller annan händelse).
Triangel-sprajten ska komma in från höger. Lägg in kod som gör att det kommer en ny triangel varenda gång kvadraten rör triangeln och varenda gång en triangel nått den vänstra kanten av scenen. Varje gång triangel-sprajten kommer in ska en ny klädsel användas.
Ett hopp där kvadraten hoppar över triangeln utan att röra den räknas som ett lyckat hopp. Gör en variabel som räknar antalet lyckade hopp.
Bestäm själv vilken funktionalitet spelet ska ha och när spelaren vunnit. Spelaren kan ha vunnit efter ett visst antal lyckade hopp eller efter att det gått en viss tid. Bestäm själv om spelaren ska kunna förlora och vad en förlust innebär. Bestäm själv vad som ska hända vid vinst eller förlust.
Hopp med gravitation
Modellera någon sorts hopp med gravitation där någon sprajt rör sig längs en parabel. Bestäm själv vad ditt program ska handla om. Ett exempel är en variant av Angry Birds där man exempelvis kan använda kloner som kastas iväg.

Flappy Bird
Flappy Bird är ett spel som slutade tillverkas eftersom spelets skapare tyckte att spelet var för beroendeframkallande. I Flappy Bird ska en fågel flyga mellan ett par rör utan att nudda dem. Det kommer hela tiden nya par rör. Fågeln faller hela tiden neråt men får en knuff uppåt och flaxar till när spelaren klickar på skärmen. När fågeln tagit sig igenom ett par rör får spelaren ett poäng. Om fågeln rör vid rören eller den nedra kanten är spelet över. Spelet går ut på att få så många poäng som möjligt.
Gör en egen variant av Flappy Bird i Scratch.

Rekursion ‐ Snöflinga
Den svenske matematikern Helge von Koch har givit namn åt en av de mest kända fraktalerna, den så kallade Koch-kurvan. Helge von Koch beskrev Koch-kurvan redan år 1904, långt innan datorer kunde användas för att rita kurvan. Det går att rita en Koch-kurva för hand men det krävs en viss tålmodighet.
Läs beskrivningen av Koch-kurvan på Wikipedia, eller annan beskrivning. Gör sedan ett eget block i Scratch som ritar en Koch-kurva med hjälp av rekursion.

Använd ditt block för att göra en Koch-snöflinga. Snöflingan görs på samma sätt som man i Scratch ritar en liksidig triangel, fast istället för att rita tre triangelsidor ritar man tre Kock-kurvor.

Rekursion ‐ Valfritt
Gör ett valfritt program som använder rekursion. Det är exempelvis vanligt att rekursion används för att göra träd.
För att få inspiration och se hur andra gör kan du använda sökrutan i Scratch och exempelvis söka på "tree" eller "fractal". Det går också att få inspiration av universitetet Berkeley och deras blockprogrammeringgspråk Snap. Snap används som introduktion i programmering för vuxna och innehåller viss funktionalitet som är mer avancerad än Scratch.